A Baccarat Promotion Designed for Advantage Players

By Anonymous
|
|
Recently I became aware of a very unusual baccarat promotion when details about it were posted on the Wizard of Vegas website (see this thread). What was especially odd was that the post was made by a well-known high-level advantage player (who goes by the moniker ssho88). This AP was seeking confirmation of computational results made by a member of his team. In fact, he specifically asked for me to double-check his teammate's work. Naturally, I agreed. As long as the AP understands that my work will be posted in a public forum, I have no problem with such requests. I can only surmise that by the time this post is published, his team will have completed their play and will be several hundred thousand dollars richer and many miles away.
The way the promotion works is as follows. The player buys $60,000 in ordinary chips. He is then given a bonus of $30,000 additional chips. This sounds great, but there's a catch. The player can never cash out these chips. He can only cash out any money he wins in excess of $90,000. But, the player is welcome to cash out this excess as often as he wishes. That is, every time the player's bankroll exceeds $90,000, he can cash out the difference (currentBankroll - $90,000) so that his bankroll once again becomes $90,000. The player plays until he loses his entire $90,000 initial bankroll. Losing the entire $90,000 is inevitable; baccarat wagers have a house edge, after all.
Sometimes the AP will just start losing and never get above $90,000. In this case he will lose his original $60,000 stake, and too bad for the AP. But, gambling is a random walk and it is quite likely the AP will be ahead (more than $90,000) at some point. Because the AP is given an extra $30,000 to cushion the negative swings, he is able to generate positive expected value if he can make large enough wagers to generate enough volatility. In the case of this promotion, ssho88 stated that the table limits allowed wagers up to $10,000.
It follows that there are two strategies that an AP will take against this promotion that a typical player may not do. These are:
The following table shows the statistical results for 16 different simulations I ran. I assumed the AP used the strategy of always cashing out any winnings above the original $90,000 (if any) after each hand.
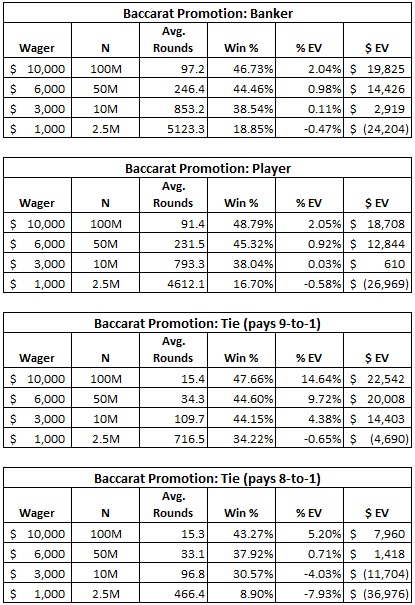
For example, consider the AP who wagers $10,000 on Banker each hand:
In particular, ssho88 stated that his team was going to buy into this promotion 20 times. It follows that his team expects to earn 20 x $18,708 = $374,160 in net profit. Wow!
It should come as no surprise that the AP earns more by wagering more. Likewise, because the house edge on Banker is lower than Player, the AP earns more by wagering on Banker than Player for a fixed wager size. What does come as a surprise (at least to me) is that in the case that the Tie bet pays 9-to-1 (as it does in some international jurisdictions), then the win-rate on the Tie bet against this promotion exceeds both the Banker and Player bet.
By reference to the table above, here are the statistics for playing against this promotion by making $10,000 wagers on the Tie bet, given that the Tie bet pays 9-to-1:
Three things:
The way the promotion works is as follows. The player buys $60,000 in ordinary chips. He is then given a bonus of $30,000 additional chips. This sounds great, but there's a catch. The player can never cash out these chips. He can only cash out any money he wins in excess of $90,000. But, the player is welcome to cash out this excess as often as he wishes. That is, every time the player's bankroll exceeds $90,000, he can cash out the difference (currentBankroll - $90,000) so that his bankroll once again becomes $90,000. The player plays until he loses his entire $90,000 initial bankroll. Losing the entire $90,000 is inevitable; baccarat wagers have a house edge, after all.
Sometimes the AP will just start losing and never get above $90,000. In this case he will lose his original $60,000 stake, and too bad for the AP. But, gambling is a random walk and it is quite likely the AP will be ahead (more than $90,000) at some point. Because the AP is given an extra $30,000 to cushion the negative swings, he is able to generate positive expected value if he can make large enough wagers to generate enough volatility. In the case of this promotion, ssho88 stated that the table limits allowed wagers up to $10,000.
It follows that there are two strategies that an AP will take against this promotion that a typical player may not do. These are:
- Wager the table maximum ($10,000).
- Cash out the excess each hand, if possible.
The following table shows the statistical results for 16 different simulations I ran. I assumed the AP used the strategy of always cashing out any winnings above the original $90,000 (if any) after each hand.

For example, consider the AP who wagers $10,000 on Banker each hand:
- 100,000,000 (100M) APs were simulated and their results averaged together.
- On average, the number of rounds the AP plays before going broke is 97.2
- The percentage of APs who will make money on this promotion (cash out a total of more than $60,000) is about 48.79%. Another view of this number is that the probability the AP beats the house is about 0.4879.
- The expected win for each AP is about $18,708. This number means that on average the AP's initial $60,000 investment will return $18.708 in profit (cash out a total of $78,708), for an average 31.18% profit on his stake.
In particular, ssho88 stated that his team was going to buy into this promotion 20 times. It follows that his team expects to earn 20 x $18,708 = $374,160 in net profit. Wow!
It should come as no surprise that the AP earns more by wagering more. Likewise, because the house edge on Banker is lower than Player, the AP earns more by wagering on Banker than Player for a fixed wager size. What does come as a surprise (at least to me) is that in the case that the Tie bet pays 9-to-1 (as it does in some international jurisdictions), then the win-rate on the Tie bet against this promotion exceeds both the Banker and Player bet.
By reference to the table above, here are the statistics for playing against this promotion by making $10,000 wagers on the Tie bet, given that the Tie bet pays 9-to-1:
- On average, the number of rounds the AP plays before going broke is 15.4
- The percentage of APs who will make money on this promotion (cash out a total of more than $60,000) is about 47.66%.
- The expected win for each AP is about $22,542.
Three things:
- If you are an AP and you have not yet burned it out, you are not going to make many AP friends by posting about it on a public board (especially one I read).
- If you are a casino trying to be creative attracting high-level play in a competitive environment, don't be surprised when APs crush you.
- If this is your casino, please don't fire the person whose idea this was. Rather, refocus on educating everyone in your casino.


