The Mathematics of Baccarat Non-Negotiable Chip Programs

By Anonymous
|
|
While much of the U.S. market shuns baccarat, it is the number one game internationally. The size of the wagers players make is stunning to watch. In Macau, for example, it is difficult to find a table with a minimum wager less than $100. The casinos are packed full of what we in America would consider to be high-rollers. And marketing understands that high-rollers want perks and cash-incentives for their play. Asian casinos use an essentially perfect solution to line up theoretical win with cash-incentive: non-negotiable chips (NN). The amount returned to the player as a cash-incentive corresponds to a cash rebate on the non-negotiable chips purchased and lost by the player.
I am often faced with situations where a baccarat player has been beating NN chip programs for a period of years, or is up a substantial amount over a brief period of time. When the question of advantage play or cheating comes up, the first thing I like to do is present a risk analysis report for the player. This involves figuring out the likelihood of achieving a result like the player’s just by chance. It almost always turns out that what appears very unlikely to the casino is well within the normal risks associated with offering games of chance. Some players get lucky. But when a high-roller is the one getting lucky, regardless of what the math says, casino executives sometimes have a hard time believing everything is on the square.
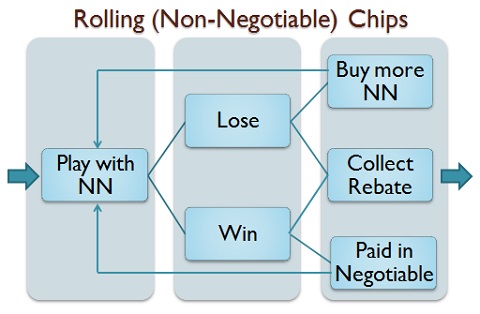
Here is a summary of how NN rolling chip programs work:
The following image illustrates the flow of NN rolling chip programs:
As an example of a player using a rolling chip program, consider a player who is using $10,000 denomination NN chips with a 1% rolling chip rebate. He plays for some period of time, during which he purchases 200 NN chips. At the end of the session he returns unused 48 NN chips. The player lost 152 NN chips. These 152 chips have a total cash value of 152 x $10000 = $1,520,000. The player’s cash rebate is 1% of this value, or $15,200. That’s all there is to it.
In some casinos and jurisdictions, NN chips are not allowed to be returned. In this case, the cash-discount can be given up front. This method is often referred to as playing with “dead chips.” In the situation given in the previous example, a player who purchased 200 dead chips with a denomination of $10,000 would be given a cash rebate of $20,000 on his $2,000,000 purchase. The player is not allowed to return his unused NN chips for cash.
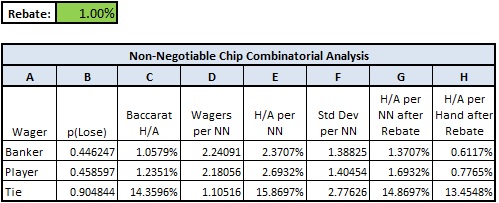
I now present the combinatorial analysis for NN chips and cash rebates, as illustrated in the examples above. I am going to show you the analysis first and explain it afterwards, one column at a time. Here it is:
If you want to follow a
long with this spreadsheet or any of those that follow, you can download everything here:
Non_Negotiable_CA
[Here is a spreadsheet version that includes tables that exclude ties: Non_Negotiable_CA_Rev_01]
Here are the explanations for each column.
So that’s it, the combinatorial analysis for NN chip programs. I have a couple of comments and examples I want to give. First, the key numbers in the table above for the industry are those given in Column E. When a player uses an NN chip, the casino wants to know how much T-Win it has earned. The values 2.37%, 2.69% and 15.87%, represent the theoretical-win (T-win) for each NN chip played and lost on the Banker, Player or Tie wagers, respectively. However, in the actual casino world, these double-digit decimal values are not used. Instead, you will hear casino management speak of winning 2.8%, or 3% per NN chip (or some other value their casino has agreed upon). These percentages are a rough blend of the three baccarat wagers, but do not have any formal theoretical meaning.
For example, if a player wagers (plays till he loses) a $10,000 NN chip on Banker, a casino that uses the 3% number will award this player a T-Win of $300 for his play, whereas his actual T-Win is $237. This means that the player is being awarded 26.6% more T-Win than he actually generated. It follows that an advantage player may be able to exploit an NN chip program that makes overly generous assumptions about the H/A per NN.
Another way to view NN chip programs is in terms of the fraction of T-Win being returned as cash to the player. For example, consider a player who wagers and loses 100 NN chips of denomination $10,000 and is given a 1.25% rebate on his NNs. His rebate is then 1.25% x 100 x $10,000 = $12,500. Assume this player lost 50 of his NN’s on Banker bets, 45 of them on Player bets and 5 of them on Tie bets. Then the casino’s effective house edge per NN used is 3.1908%, as illustrated in the following computation:
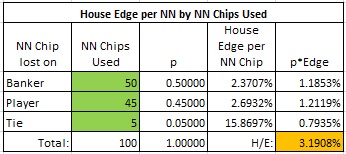
It follows that the player’s T-Win was 3.1908% x 100 x $10,000 = $31,908. Therefore, the casino is returning $12,500/$31,908 = 39.2% of this player’s T-Win as a straight cash rebate.
I have personal experience with rebate percentages as high as 1.6%. Anecdotally, I have heard that rebates up to 1.8% are not uncommon. I have one report of a rebate of 2.0% being given to a high-roller. In the example above, if this player was given a 2.0% rebate, then the amount returned to him would have been $20,000. With a 2.0% rebate, $20,000/$31,908 = 62.7% of this player’s T-Win would be given back to him as a straight cash rebate. If he was an advantage play, making only Banker bets, then $20,000/$23,707 = 84.4% of this player’s T-Win would be given back to him as a straight cash rebate. This is clearly an untenable relationship for the casino.
Another way to measure the cost of NN chip programs is by the reduction in the house edge per hand incurred by the cash rebates. The following table gives the effective house edges for the Banker, Player and Tie wagers per hand, for a variety of rebate percentages:
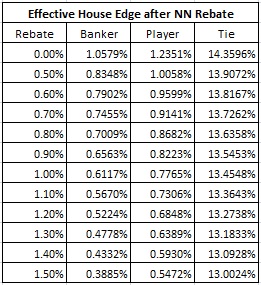
These reductions in house edge occur without a corresponding change in the standard deviation. For this reason, there is considerable risk involved in giving NN rebates, as I will demonstrate in a subsequent blog post.
What makes NN chip cash rebates so valuable from the casino side is that they give back a fixed percentage of T-Win back to the player. This value can be accurately accounted with the theoretical models given above. There is no need for the casino to record the time played or average bet of the player. That’s all part of reconciling the number of NN’s lost. These rebates are the beginning and end of what most high-rolling Asian players get back for their play. And they like it.
By contrast, the U.S. market is full of non T-Win based cash-incentives (e.g. loss rebates, quick losses, show-up money, front money, promotional chips and quick pay). Abuse of non T-win based incentives is common. Players keep expecting more and the casinos comply in order to keep up with their competitors. The concept of tying the incentive to a percentage T-Win breaks down in the U.S. model. Many casinos do an extraordinarily poor job of evaluating the T-Win for their high-rollers. They have no idea about the true worth of their premium customers or the percentage of that worth being returned to the player in cash or other incentives. Getting upside down with players is a frequent occurrence. This flawed incentive model creates advantage players like Don Johnson (the tip of the iceberg) who beat the loss-rebate incentives he received outright.
In my opinion, the U.S. market has a lot of maturing to do when it comes to re-investing in their high-rollers. In short, it’s a mess. NN programs give clear guidance on an effective cash-incentive program that can be utilized for high-rollers across any number of games. What works for baccarat also works for blackjack. NN chips should become the default currency used by high-roller marketing programs.
I am often faced with situations where a baccarat player has been beating NN chip programs for a period of years, or is up a substantial amount over a brief period of time. When the question of advantage play or cheating comes up, the first thing I like to do is present a risk analysis report for the player. This involves figuring out the likelihood of achieving a result like the player’s just by chance. It almost always turns out that what appears very unlikely to the casino is well within the normal risks associated with offering games of chance. Some players get lucky. But when a high-roller is the one getting lucky, regardless of what the math says, casino executives sometimes have a hard time believing everything is on the square.
Here is a summary of how NN rolling chip programs work:
- The player purchases non-negotiable chips (NN) with cash. The chips are purchased at their face value. For example, a $10,000 chip costs exactly $10,000 to purchase.
- The casino keeps track of all of the non-negotiable chip purchase the player makes.
- The player only wagers NN chips. He does not wager cash or ordinary casino chips. If the player does wager ordinary chips, no rebate is awarded based on those wagers.
- If the player wins, he is paid in ordinary chips corresponding to the NN chips he wagered. If he loses, the NN chips he wagered are collected.
- It follows that the more the player plays, the more cash chips he collects for the hands he wins, while his stack of NN chips decreases every time he loses a hand.
- Any time the player wants, he can purchase more NN chips. He purchases these chips either using cash, or using cash chips he has won during his play.
- The player continues to purchase and play NN chips, using his ordinary winnings or cash to buy more chips.
- At the end of his session, the player redeems his unused NN chips for cash at their face value.
- The casino subtracts the NN chips returned from the NN chips purchased to determine the chips lost. The player is then given a cash rebate which is a fixed percentage of the total cash value of the number of NN chips played and lost.
The following image illustrates the flow of NN rolling chip programs:

As an example of a player using a rolling chip program, consider a player who is using $10,000 denomination NN chips with a 1% rolling chip rebate. He plays for some period of time, during which he purchases 200 NN chips. At the end of the session he returns unused 48 NN chips. The player lost 152 NN chips. These 152 chips have a total cash value of 152 x $10000 = $1,520,000. The player’s cash rebate is 1% of this value, or $15,200. That’s all there is to it.
In some casinos and jurisdictions, NN chips are not allowed to be returned. In this case, the cash-discount can be given up front. This method is often referred to as playing with “dead chips.” In the situation given in the previous example, a player who purchased 200 dead chips with a denomination of $10,000 would be given a cash rebate of $20,000 on his $2,000,000 purchase. The player is not allowed to return his unused NN chips for cash.
I now present the combinatorial analysis for NN chips and cash rebates, as illustrated in the examples above. I am going to show you the analysis first and explain it afterwards, one column at a time. Here it is:

If you want to follow a
long with this spreadsheet or any of those that follow, you can download everything here:
Non_Negotiable_CA
[Here is a spreadsheet version that includes tables that exclude ties: Non_Negotiable_CA_Rev_01]
Here are the explanations for each column.
- (Column A) Wager: This is simply the wager the player makes with his NN chip.
- (Column B) P(Lose): The player continues to use the NN until he loses it, so this information is recorded for use later in the table. This data is retrieved directly from the combinatorial analysis for baccarat. A Banker wager loses whenever the result of the hand is Player. A Player wager loses whenever the result of the hand is Banker. A Tie wager loses whenever the result of the hand is Banker or Player.
- (Column C) Baccarat H/A: These values are just the house edges for each wager, as computed in the combinatorial analysis of baccarat.
- (Column D) Wagers per NN: This column gives the average number of times an NN chip is wagered on the given bet before it is lost. In column B, I gave the probability of losing an NN chip. So column C is simply the reciprocal of those values. That is, if an event has probability p of occurring, then it happens on average once every 1/p times the game is played.
- (Column E) H/A per NN: This column gives the percent of the value of each NN chip used that is theoretically won by the house. NN chips can be wagered multiple times. Each time an NN chip is wagered, the casino earns its house edge on that wager. It follows that the H/A per NN is simply the product of the house edge for the wager times the number of times the chip is used on that wager. In other words, the Column E is the product of Column C and Column D.
- (Column F) Standard Deviation per NN: The standard deviation for each baccarat wager is given under the combinatorial analysis tab. If a wager is made multiple times, say X times, then you multiply the standard deviation for making the wager one time by sqrt(X) to get the resulting standard deviation. Hence the values in Column F are equal to the square root of the values in column D times the standard deviations taken from the Baccarat_CA tab.
- (Column G) H/A per NN after Rebate: The rebate percentage is input by the user (it is shaded in green). This interactive input allows the user to obtain statistical information about his NN program. Column G simply subtracts the rebate percentage input by the user from the values in column E.
- (Column H) H/A per Hand after Rebate: The house edge per NN after the cash rebate appears in Column G. The number of hands per NN is given in Column D. This column simply divides the values in Column G by those in Column D.
So that’s it, the combinatorial analysis for NN chip programs. I have a couple of comments and examples I want to give. First, the key numbers in the table above for the industry are those given in Column E. When a player uses an NN chip, the casino wants to know how much T-Win it has earned. The values 2.37%, 2.69% and 15.87%, represent the theoretical-win (T-win) for each NN chip played and lost on the Banker, Player or Tie wagers, respectively. However, in the actual casino world, these double-digit decimal values are not used. Instead, you will hear casino management speak of winning 2.8%, or 3% per NN chip (or some other value their casino has agreed upon). These percentages are a rough blend of the three baccarat wagers, but do not have any formal theoretical meaning.
For example, if a player wagers (plays till he loses) a $10,000 NN chip on Banker, a casino that uses the 3% number will award this player a T-Win of $300 for his play, whereas his actual T-Win is $237. This means that the player is being awarded 26.6% more T-Win than he actually generated. It follows that an advantage player may be able to exploit an NN chip program that makes overly generous assumptions about the H/A per NN.
Another way to view NN chip programs is in terms of the fraction of T-Win being returned as cash to the player. For example, consider a player who wagers and loses 100 NN chips of denomination $10,000 and is given a 1.25% rebate on his NNs. His rebate is then 1.25% x 100 x $10,000 = $12,500. Assume this player lost 50 of his NN’s on Banker bets, 45 of them on Player bets and 5 of them on Tie bets. Then the casino’s effective house edge per NN used is 3.1908%, as illustrated in the following computation:

It follows that the player’s T-Win was 3.1908% x 100 x $10,000 = $31,908. Therefore, the casino is returning $12,500/$31,908 = 39.2% of this player’s T-Win as a straight cash rebate.
I have personal experience with rebate percentages as high as 1.6%. Anecdotally, I have heard that rebates up to 1.8% are not uncommon. I have one report of a rebate of 2.0% being given to a high-roller. In the example above, if this player was given a 2.0% rebate, then the amount returned to him would have been $20,000. With a 2.0% rebate, $20,000/$31,908 = 62.7% of this player’s T-Win would be given back to him as a straight cash rebate. If he was an advantage play, making only Banker bets, then $20,000/$23,707 = 84.4% of this player’s T-Win would be given back to him as a straight cash rebate. This is clearly an untenable relationship for the casino.
Another way to measure the cost of NN chip programs is by the reduction in the house edge per hand incurred by the cash rebates. The following table gives the effective house edges for the Banker, Player and Tie wagers per hand, for a variety of rebate percentages:

These reductions in house edge occur without a corresponding change in the standard deviation. For this reason, there is considerable risk involved in giving NN rebates, as I will demonstrate in a subsequent blog post.
What makes NN chip cash rebates so valuable from the casino side is that they give back a fixed percentage of T-Win back to the player. This value can be accurately accounted with the theoretical models given above. There is no need for the casino to record the time played or average bet of the player. That’s all part of reconciling the number of NN’s lost. These rebates are the beginning and end of what most high-rolling Asian players get back for their play. And they like it.
By contrast, the U.S. market is full of non T-Win based cash-incentives (e.g. loss rebates, quick losses, show-up money, front money, promotional chips and quick pay). Abuse of non T-win based incentives is common. Players keep expecting more and the casinos comply in order to keep up with their competitors. The concept of tying the incentive to a percentage T-Win breaks down in the U.S. model. Many casinos do an extraordinarily poor job of evaluating the T-Win for their high-rollers. They have no idea about the true worth of their premium customers or the percentage of that worth being returned to the player in cash or other incentives. Getting upside down with players is a frequent occurrence. This flawed incentive model creates advantage players like Don Johnson (the tip of the iceberg) who beat the loss-rebate incentives he received outright.
In my opinion, the U.S. market has a lot of maturing to do when it comes to re-investing in their high-rollers. In short, it’s a mess. NN programs give clear guidance on an effective cash-incentive program that can be utilized for high-rollers across any number of games. What works for baccarat also works for blackjack. NN chips should become the default currency used by high-roller marketing programs.


