High Card Flush Collusion

High Card Flush (HCF)  is a relatively new game that distinguished itself by winning “Best Game” at the Cutting Edge Table Games Conference in 2012. Recently Stephen How demonstrated that HCF has a significant collusion issue (see this post at his blog, discountgambling.net). With six players at the table sharing full information about their hands (colluding), he stated that these players could each get a 7.3% edge over the house. He gave a practical strategy that yielded a 3.1% player edge. This post presents my analysis of collusion advantage play against HCF.

 

The rules for HCF are fairly easy to understand. They use the familiar Ante/Raise structure.

 

1. The player makes an “Ante” wager.

2. The player and the dealer receive seven cards, face-down.

3. The player makes the highest ranking flush from his seven cards. To rank flushes, the following two criteria are used. Flushes are first ranked by the number of cards used in the flush. The more cards, the higher the rank. Flushes with the same number of cards are ranked by their highest card(s).

4. The player can then fold and surrender his Ante or can make a Play bet to compete against the dealer.

5. The Play bet amount depends on the number of cards in the players flush. 1x with a two, three or four-card flush. 2x with a five-card flush. 3x with a six or seven-card flush.

6. The dealer then turns over his cards and makes his best flush. The dealer needs at least a nine-high three card flush or better to qualify.

7. If the dealer does not qualify, the Ante bet wins even money and the Play bet pushes.

8. If the dealer qualifies then the player and dealer compete. If the player wins, his Ante and Play bets are paid even money.  If the player loses, he forfeits his Ante and Play bets.  If the player and dealer push, then the Ante and Play bets push.

 

The HCF tables I have seen have spots for six players. Because seven cards are dealt to each hand, a full table will require 42 cards for the player hands. This leaves only ten (10) unknown cards from which the dealer will select seven for his hand. I will call these 10 cards the “remainder.” The small size of the remainder is what gives collusion its power in HCF.

 

The following table is based on a simulation of two billion (2,000,000,000) rounds of HCF, where the players use perfect collusion strategy. This strategy is unknowable in any practical sense. My program computed optimal strategy on-the-fly for each hand.

 

 

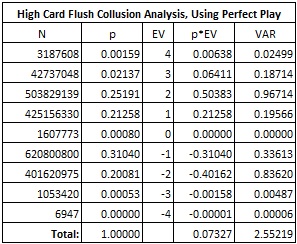
In particular:

 

• The player edge from perfect six-player collusion is 7.327%.

• The standard deviation from perfect six-player collusion is 1.598.

 

I note that perfect five-player collusion gives a house edge of about 0.61%. There is simply not enough information available to overcome the house edge.  In other words, an edge is not possible with five or fewer colluding players at the table.

 

A high-edge, low volatility game is precisely what APs look for, and HCF appears ripe for the picking. Unfortunately for the AP, there is a practical problem. The perfect strategy that gives the AP a 7.327% edge is unknown. In Stephen How’s blog article, he gives a simple strategy for the AP that yields a player edge of about 3.1%. In due respect for How's excellent research, I won’t repeat his strategy here. Instead, I am going to present a somewhat tougher strategy that yields a return over 4% for the AP.

 

Suppose a team of six APs are at the table. Four of them are assigned to count the suits. There is an AP assigned to “clubs”, one to “diamonds”, one to “hearts” and one to “spades.” The team of six APs shows their cards to each other. Each of the four APs counts the number of cards they see in their respective suit. By doing so, each will arrive at a number from 0 to 13. By subtracting their number from 13, they will get the number of cards of their respective suit in the remainder.  This is the number they report to each other.

 

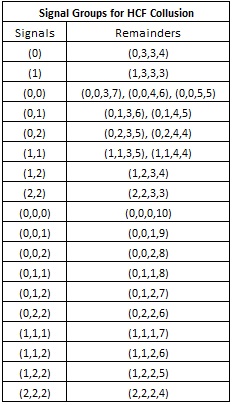
Note that the four numbers determined by the APs together must sum to 10 (there are 10 cards in the remainder, after all). Here is a complete list of the twenty-three possible suit distributions:

 

(0,0,0,10), (0,0,1,9), (0,0,2,8), (0,0,3,7), (0,0,4,6), (0,0,5,5), (0,1,1,8), (0,1,2,7), (0,1,3,6),  (0,1,4,5),  (0,2,2,6),  (0,2,3,5),  (0,2,4,4), (0,3,3,4), (1,1,1,7), (1,1,2,6), (1,1,3,5), (1,1,4,4), (1,2,2,5), (1,2,3,4), (1,3,3,3), (2,2,2,4), (2,2,3,3).

 

An impractical approach is to give a threshold flush for each of these distributions. In other words, play a given hand or higher depending on the specific distribution from this list. Stephen How understood that this is too much information to convey at the table in real-time.  His simple strategy selected a small subset of these distributions and gave a threshold for each. My approach also takes into account that a collusion strategy must be human feasible. However, I will require more effort from the APs.

 

Imagine an AP counting his given suit and trying to convey that information in real-time to the other APs at the table. What is he going to do?  He’s not going to say his number out loud. Also, he doesn’t want to pile some number of chips, from 0 to 10, in front of him to signal his suit count. The method I present requires that the AP signal only the numbers 0, 1, or 2, or else not signal at all.

 

Here’s how it works. If the AP determines that there are 0, 1 or 2 of his suit in the remainder, then he signals that number to his team. If the AP determines that there are 3 or more of his suit in the remainder, then he does not signal.  An AP could discretely signal these values, for example, by touching one of three fingers on his right hand with his right thumb. Or he could make a pile of 0, 1, 2 chips, or no pile at all. Or scratch one of three parts of his face (or not scratch). And so on.

 

In other words:

 

• If the AP observes 10 or fewer of his suit in the six hands, then he does not signal.

• If the AP observes 11 of his suit, then he signals “2”.

• If the AP observes 12 of his suit, then he signals “1”.

• If the AP observes 13 of his suit, then he signals “0”.

 

There are then 18 possibilities for the groups of signals the APs can give. The following table lists these 18 signal groups, together with the remainders that pertain to each:

 

 

Collusion strategy is based on the signal group the APs determine with their four individual signals. The following table gives collusion strategy for the 18 possible signal groups. I make no claim that this strategy is optimal. I did a lot of “rounding” in the strategy to make the decision points as easy as possible to remember.

 

 

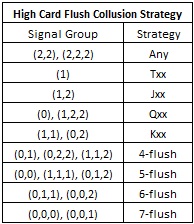
For example, if the signal group is (2, 2 ,2), then the colluding APs should play any hand. If the signal group is (1, 2, 2), then the APs should play a Queen high 3-flush or higher. If the signal group is (0,1,2), then any hand less than a 5-flush should be folded.

 

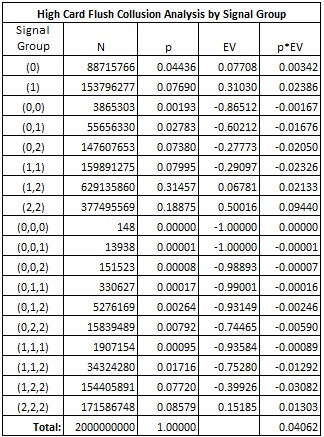
The following table is based on a simulation of two billion (2,000,000,000) rounds of HCF, where the APs use the signal group collusion strategy given above:

 

 

The following table is based on the same simulation of two billion (2,000,000,000) rounds of HCF, where the APs use the signal group collusion strategy. This table is a more traditional combinatorial analysis. It groups the outcomes by the number of units won or lost:

 

 

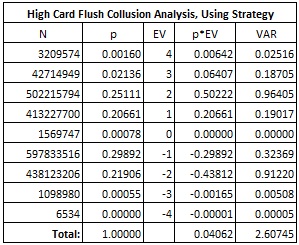
In particular,

 

• The AP has an edge of 4.062% over the house.

• The standard deviation is 1.615.

• The group (2,2) is the most player favorable, with an expected return of 0.502 units.

 

To get an idea of the earning potential, assume six APs occupy a HCF table with a table limit of $100 and that the game pace moves at 40 rounds per hour. Then the APs will win a combined (40) x (6) x ($100) x (4.062%) = $975 per hour from the table. With a $100 max bet, this is probably not worth it for most AP teams. But a table limit of $500 would certainly draw top APs, giving a table-yield of nearly $5000 per hour to the team.

 

Obviously, folding any 4/5/6-flush is going to look very funny to anyone watching the game. Longevity implies that it will be best to never fold these hands.  The cover strategy of never folding a 4-flush or better is as follows:

 

 

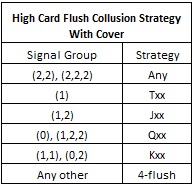
Very little EV is lost using the cover strategy.  The following table is based on a simulation of one billion (1,000,000,000) rounds of HCF, using the collusion strategy with cover given above:

 

 

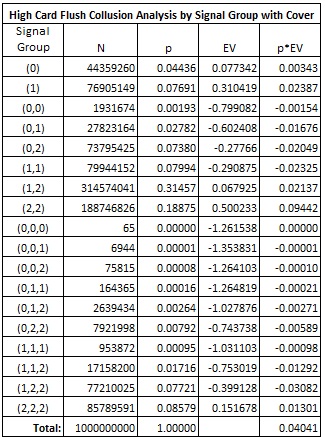
In particular, the AP has an edge of 4.041% over the house using this strategy. The cover strategy is only about 0.02% weaker than the full collusion strategy and is still nearly 1% higher than How's strategy.

 

Any casino that offers HCF should be informed of its vulnerability and game protection solutions should be put in place.  Here are some suggestions:

 

• Don’t worry if five or fewer players are playing.

• Reduce the number of play locations from six to five.

• Don’t allow players to look at each other’s hands or share information about their hands.

• Watch for the situation when every seat is occupied and players are playing at or near the table maximum and are sharing information.

• Watch for signals between players.

• Watch for any other indication that a team is playing against the game.