Ultimate Three Card Poker Hole-Card Play

By
|
|
Apheat, Novelty Games
The game of Ultimate Three Card Poker is a version of Three Card Poker where the dealer exposes one of his three cards before the player acts. It may seem that this solves the ubiquitous "hole-card" problem for Three Card Poker, especially if the card that is flipped face-up is the bottom card from the three-card packet delivered by the shuffle machine. However, it is still possible that the player sees one of the two remaining dealer hole-cards. I considered how to beat the game in this unlikely circumstance. I note that I have never seen this game offered in a casino and have no idea if this opportunity actually exists.

First, a quick review of the game. The game uses a typical feature to allow extra information to be offered: a "Blind" bet. The player must make a Blind bet equal to his Ante. The Blind bet is then paid according to a pay table if the player's winning hand is sufficiently strong. Otherwise, the Blind pushes or loses. Here are the rules:

 

  1. The player makes equal bets in the Ante and Blind circles.

  2. The player and dealer each receive three cards and the dealer will turn one card face-up.

  3. The player may then fold or make a Play bet to compete against the dealer.

  4. The Play bet must equal the Ante unless the player has a pair or better. In this case, the player may bet 3x his Ante.

  5. The dealer then exposes his remaining two cards and the bet is settled as follows.

  6. Ante bet: if the dealer has less than Queen high, the Ante bet pushes. Otherwise the Ante bet wins/loses/pushes by comparing the dealer and player hands.

  7. Play bet: This bet wins/loses/pushes by comparing the dealer and player hands. There is no qualifying hand for this bet.

  8. Blind bet: This bet wins/loses/pushes by comparing the dealer and player hands. There is no qualifying hand for this bet. The amount won is determined by a pay table; the minimum hand required for a winning payout is a player Flush.


Here is the pay table for the Blind bet:
 

  1. Mini-royal (AKQ suited) pays 100-to-1.

  2. Straight Flush pays 8-to-1.

  3. Three of a Kind pays 6-to-1.

  4. Straight pays 3-to-2.

  5. Flush pays 1-to-1.

  6. All other hands push.


I first noticed this game in a post made by Stephen How at his website www.discountgambling.net. Stephen gives a basic strategy for this bet and states that the house edge is 3.8807% with optimal play. I began this project by confirming Stephen's house edge and our results agree exactly. However, my basic strategy is slightly different from his. After speaking with Stephen about this, his strategy is for a fixed suit distribution; he stated that the three cards were assumed to be of different suits in his basic strategy. My strategy is the lowest hand to play among all suit distributions. Needless to say, using either strategy will lead to a house edge in practice that is greater than 3.8807%. Complete basic strategy would have to identify the suits of all cards.
 

  • Upcard 2, play 9/5/2 or better

  • Upcard 3, play 9/7/3 or better

  • Upcard 4, play 9/8/4 or better

  • Upcard 5, play 9/8/5 or better

  • Upcard 6, play 9/8/6 or better

  • Upcard 7, play 9/7/6 or better

  • Upcard 8, play 9/8/5 or better

  • Upcard 9, play 9/8/3 or better

  • Upcard T, play T/8/3 or better

  • Upcard J, play J/8/3 or better

  • Upcard Q, play Q/8/3 or better

  • Upcard K, play K/8/3 or better

  • Upcard A, play A/8/5 or better

  • Always raise 3x with a pair or better


I then considered what happens when the player can see a second card. On Stephen's site, he states that an individual named "Jet" has a hole-card strategy that yields an edge of 9%. I wrote a program that first computed perfect hole-card strategy and I came up with a  player edge of 8.9544%. Unfortunately, perfect hole-card strategy is quite complicated and I didn't attempt to quantify it for practical use.

A simple-minded approach is to give, for each pair d1/d2 of dealer cards, a minimum player hand p1/p2/p3 such that the player should play that hand or higher. Using the strategy below, the player edge is 8.9431%. This human-doable strategy is 0.0113% from being optimal.  In this table, p = pair, s = suited, o = off-suited.

If the player has a qualifying pair or better according to this strategy, then the player always raises 3x when using this strategy. This is not entirely correct advice for optimal hole-card play. For example, in the hand 2/2p, the player should raise 1x holding y/2/2 for several values of y. But these exceptions are rare and not worth the extra effort.
 
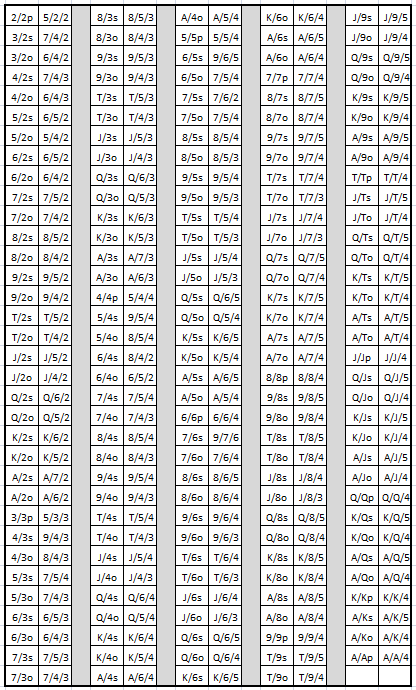
Hole Card Strategy

Like many other proprietary games, exposing a hole-card is one of the most significant opportunities an AP can find. Many games have extremely complex hole-card strategies. Although the strategy above is a challenge (at least it would be for me) to learn, most of the hands follow an intuitive strategy that repeats for many other hands. The best solution for the casino to protect this game is to frequently audit hole-card exposure on all proprietary games. Of course, positioning the shuffler properly is also a critical part of game protection.