Card Counting the Dragon/Fortune 7 Baccarat Side Bet

I first considered if the Dragon 7 baccarat side bet was susceptible to a card counting methodology in mid-2011 when it was exclusively a proprietary side bet owned by DEQ that was associated with the commission free baccarat variant EZ Baccarat. Since that time, the patent for both EZ Baccarat and the Dragon 7 bet have expired (see this post). Naturally, Shuffle Master (SHFL, Bally, whatever) pounced on the opportunity to grab the intellectual property. They re-branded the Dragon 7 as the "Fortune 7" bet and are now actively marketing it as their own product. Ah, capitalism!

 

The Dragon/Fortune 7 baccarat side bet (DF7) is simple to describe. This side bet pays 40-to-1 if the Banker’s three-card total of 7 wins the hand, otherwise the bet loses. Analysis of the wager consists of a straight forward cycle through all possible hands. The table below gives the analysis for eight decks.

 

 

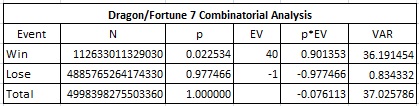
In particular,

 

• The house edge is 7.6113%.
• The standard deviation is 6.0849.
• The hit frequency is 2.2534%.

 

When I first thought about the possibility of card counting DF7 in the summer of 2011, it seemed as though DF7 was more probable to hit if there was an excess of 7 and 10 valued cards in the deck. In this case, the dealer would be more likely to draw 10-10 and hit to a 10-10-7 = 7. Later, as I read several Internet discussion boards, it became clear that others thought as I did. The conclusions were that if there was any vulnerability at all, it would come when 7’s and 10’s were in excess in the remainder of the shoe. It turns out this is not the case. DF7 is vulnerable to a card counting methodology, but the answer is surprising.

 

The key is that in order for the player to win this wager, the Banker hand has to draw a third card. This requirement trumps everything else. The cards that keep the Banker hand from drawing that third card most often are the 8 and the 9. As these cards are removed from the shoe, the edge moves quickly towards the counter’s favor. An excess of smaller cards is also helpful. The cards 1-7 are the cards that move the Banker’s final total to 7 if he draws. Since the Banker draws a third card most often with starting totals of 0, 1, 2 and 3, it follows that the cards 7, 6, 5 and 4 give three-card totals of 7 most often. Intuitively, a shoe that is rich in the cards 4, 5, 6, 7 and poor in the cards 8, 9 will favor the counter.

 

The methodology used in this study is familiar. By removing each card in turn from an eight-deck shoe, its effect on the house edge can be determined. This allows card counting systems to be developed. After arriving at candidate systems, computer simulations are run to see if these systems can generate an edge in practice. If there is an edge, the question then becomes if this is significant enough to become an opportunity for the advantage player.

 

The next table gives the effect of removal (EOR) for each card, along with two card counting systems.

 

 

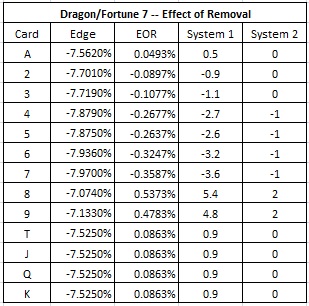
This table shows the extreme importance of ridding the shoe of 8’s and 9’s. Also, the 7 is the most important card, as expected, to remain in the shoe. The other cards diminish in value as their pips go down, presumably because they are used in fewer and fewer situations to draw to a Banker total of 7. Working against intuition, the counter’s situation improves as zero-valued cards are removed from the deck.

 

System 1 is obtained by multiplying the EOR’s by 1000. It is “optimal” in the sense that no linear card counting system can perform better. System 1 is not intended to be a practical system; its purpose is to give results to compare to a human-feasible system. System 2 is a simple card counting system based on approximating the values from system 1 to create a balanced count.

 

In summary:

 

• “System 1” has indices (0.5, -0.9, -1.1, -2.7, -2.7, -3.3, -3.6, 5.4, 4.8, 0.9).
• “System 2” has indices (0, 0, 0, -1, -1, -1, -1, 2, 2, 0).

 

To gauge the effectiveness of each, I wrote a computer program to simulate using these two systems in live play. The game I simulated has the following shuffling and cut card rules:

 

• The game is dealt from a shoe with 8 decks.
• At the start of each shoe, a card is burned. Based on the value of the burn card, an additional number of cards are burned, equal to the value of the card.
• The cut card is placed 14 cards from the end of the shoe.
• After the cut card is dealt, one more round is dealt before shuffling.

 

The following table gives card counting results for system 1 and system 2, based on a simulation of two hundred million (200,000,000) eight deck shoes, as described above:

 

 

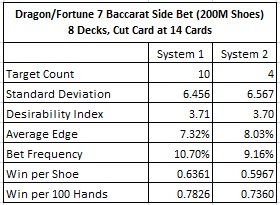
It is clear from the last row of the table above that system 2 performs remarkably well in comparison to its optimal cousin.

 

The person who uses system 2 should make the DF7 bet whenever the true count is +4 or higher. If he does so, then on average he will have an 8.03% edge over the house each time he makes the bet. This counter will have the opportunity to make the DF7 bet at or above the target true count on 9.16% of his hands. Given that the average shoe yields about 80 hands, the counter should be able to make, on average, about seven DF7 bets per shoe with the edge.

 

In dollar terms, if the house allows a DF7 bet up to $100 (say), then on a per-shoe basis the counter will average about $59.67 profit. The counter will earn about $8.03 per $100 wagered on the Dragon bet.

 

It is worthwhile to check that the simulated results for system 2 make sense combinatorially. One way to get a +4 true count off the top is to remove eight 8’s and eight 9’s from the deck. This will leave 400 cards remaining in the eight-deck shoe, with a running count of +32, for a true count of 4.16. In this case, combinatorial analysis gives a player edge of 1.0227%. Using a single deck, one way to get a +4 true count is to remove one 8 and one 9 from the deck. This leaves 50 cards with a +4 running count, giving a true count of 4.16. In this case, combinatorial analysis gives a player edge of 1.3114%. Because the player is making the Dragon bet at a true count of +4 and above, not just at +4, these computations represent a secondary confirmation of the simulated results.

 

Cut card placement varies by casino, so it is worthwhile to investigate how the edge changes with the placement of the cut card. The next table gives statistics for various cut card placements up to four decks. A cut card placement at one deck, instead of at 14 cards, decreases the potential profit to the player by about 50%.

 

 

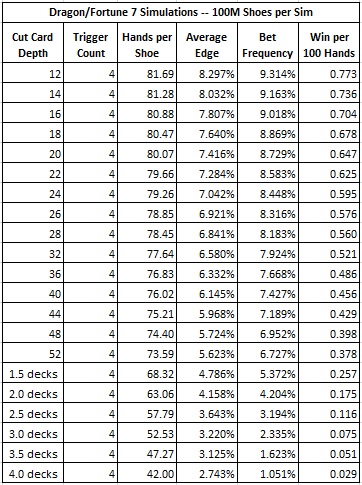
The analysis given above shows that the DF7 bet is an advantage play opportunity using a card counting methodology. Over the last few years, I have learned that individuals and teams were counting the DF7 wager before my article appeared in September, 2011 and they continue to count it today when good opportunities arise. It is not a fantasy to say that DF7 is an ongoing advantage play opportunity. But, if your casino has table maximum limit of $25 on DF7 then don’t worry about keeping your shoelaces tied.