Card Counting the Slingo Bonus Bet 21 Blackjack Side Bet

I was visiting a casino in August, 2011 when I noticed a side bet on the table I had not seen before: “Slingo Bonus Bet 21.” The bet pays purely on the total of the player’s two cards, with an Ace counting 11. I could tell right away that the bet was countable. One of the wagers the player could make was that his hand would be a blackjack. The pay table odds of 19-to-1 are near the true odds of about 20-to-1. Only a couple of extra low cards dealt out would give the player the edge. For “blackjack only” wagers, it is customary game protection to restrict the wager to the first hand dealt. On this game, the blackjack wager could be made any time through the shoe. I decided to investigate.
To play the Slingo Bonus Bet 21 blackjack side bet, the player looks at a matrix of possible wagers and can bet on any or all of them. Here are the bets the player can make and the odds each wager pays.
- Pair. Pays 12-to-1.
- Total = 17. Pays 12-to-1.
- Total = 18. Pays 14-to-1.
- Total = 19. Pays 15-to-1.
- Total = 20. Pays 8-to-1.
- Total = 21. Pays 19-to-1.
- Total = 17 or 18. Pays 6-to-1.
- Total = 18 or 19. Pays 6-to-1.
- Total = 20 or 21. Pays 5-to-1.
- Total = 17 to 20. Pays 1-to-1.
I asked the director of table games about the wager and was told that “we own it.” She said that the company had given them exclusive rights to the game and that it was offered at no other locations. I told her it was clearly vulnerable to card counting. She stated that she suspected only two APs had targeted the game since the casino installed it. I suggested the reason was the remote location of the casino and the $10 maximum on each of the 10 bets ($100 maximum total).
This bet has been around for a long time. A press release for the game from Slingo (February 1, 2006) states:
“HACKENSACK, NJ - Slingo, Inc. (Slingo) and The United States Playing Card Company (USPC) have announced a distribution agreement to bring the "Slingo Bonus Bet 21" table game to casinos world-wide.”
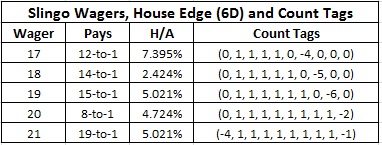
In looking at the options, it is clear that a card counter will directly target the wagers with specific totals of 17, 18, 19, 20, 21 rather than the combinations. For each of these wagers, I performed the usual computation of the house edge followed by determining the effect of removal of each card. This allowed me to come up with a reasonable balanced card counting system for each.
The table below gives the house edge and the counting system used for each bet, assuming six decks. Intuitively, the key card for the 17 wager is a 7, for 18 is an 8, for 19 is a 9, for 20 are the ten-valued cards, and for 21 is an Ace. The count systems dictated by the EORs clearly follow this intuition. As usual, the tags are listed (A, 2, 3, 4, 5, 6, 7, 8, 9, T). I make no representation that these count systems are optimal.
I then did a simulation for each of these wagers. These simulations assumed a six-deck shoe, dealt to 260 cards (cut card placed 1 deck from the end). For each, I simulated one hundred million (100,000,000) shoes. The table below summarizes the results obtained from these simulations. Here are the pertinent definitions:
- The “Trigger True Count” is the minimum true count to make the wager.
- “EV per Bet” gives the player's average edge when he makes the wager.
- “Bet Frequency” gives the percentage of time the player makes the wager.
- “Profit per 100 Hands” is profit in units for each 100 hands of blackjack.
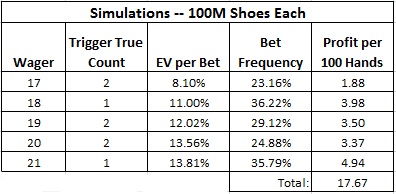
For example, a player who wagers $10 per hand on the 17 wager every time he has the edge will make this wager on 23.16% of his hands. When he makes the wager his average edge over the house will be 8.10%. The player will then earn $18.80 per 100 hands. Playing heads-up on a fast table, getting 200 rounds per hour, the player can earn $37.60 per hour making the 17 wager.
As I thought when I first saw this side bet, the best opportunity is the blackjack wager (21). A player who wagers $10 per hand on the blackjack every time he has the edge will make the wager on 35.79% of his hands. When he makes the wager his average edge over the house will be 13.81%. Simply put, on over 1/3 of the hands played the player has an average edge over 13%. The player will then earn $49.40 per 100 hands. Playing heads-up on a fast table, getting 200 rounds per hour, the player can earn $98.80 per hour making the blackjack wager.
Now consider a team of five APs who decide to count this bet. Each counter will be assigned one of these five wagers. The five will occupy the entire table, betting $10 on a wager each time they are signaled to play it by the AP who is counting that specific opportunity. Then, as the table shows, each player will earn 17.67 units per 100 hands. So, each counter will earn $176.60 per 100 hands. The team of five counters will earn $883.00 per 100 hands (if the table has 5 spots). With five players at the table, the rate of play will be about 50 rounds per hour. The game will move slowly due to all the checking and paying of the side bet. In this case, the expected hourly wage of the team will be about $441.50. This is with a maximum wager of $10. It may be the case that the APs could make the combination bets profitably as well. For example, if one AP signaled the 17 bet and another the 18 bet, then it may be profitable to play "17 or 18." I did not investigate this.
I was told that this wager was offered in Atlantic City for a brief period of time. The maximum wager per bet was $25. In this case the team described in the previous paragraph will earn just over $2,200 per 100 hands. At 50 rounds per hour, this team will earn over $1,100 per hour. I can’t verify this, but I was told that the game lasted less than a week in AC.
The analysis above is for the six-deck version. As usual, in a double-deck version, the edge the counter can obtain will be significantly higher. This side bet is the most vulnerable blackjack wager I have analyzed, by far.
How could anyone create and market a bet without knowing about this vulnerability? If they did know, how could they in good conscience try to sell this bet? How could a distributor agree to sell a bet like this without doing due-diligence on advantage play? How could a director of table games not question the vulnerability before agreeing to install it? How could a major casino in Atlantic City put a wager like this on the gaming floor? How could a little local casino not know or be told the horrors that had come before?
Come on guys!


