Blackjack Probability: What do you Need to Know to Have an Edge?
By Anonymous
|
|
When a person walks out of a casino the question that inevitably arises in their mind is “Why did I lose?” Most people that play casino games are losing players. That is because most casino games by nature have a negative expectation for the player. This means that for every wagered that is made on the game; machine or table game, gives back some amount less than the wagered amount over time.
If 1 million players wager 1 dollar and, one player wins 500K than the casino makes a profit of 500K and an average loss of 50 cents per wager is perceived. In slot machines the advertised pay back is often in the neighborhood of 97-99%. This is over the entire life of the machine where a machine may collect 100s of millions of dollars in action over its lifetime. Table games are slightly different because some include a skill component and the % advantage the casino has varies from player to player. But the same general principle applies.
This article is an in depth analysis of the mathematics of casino gaming. The information presented here is valid for live blackjack play as well as online play. However; the Blackjack software programs that online casinos use include all of the cards in every new round of play. The analysis will apply to the game of Blackjack. Blackjack is a game of dynamic probabilities and shifting percentages. But even though the percents are constantly changing, the cumulative percentage of the overall advantage remains constant.
This is achieved by taking the sum of the advantages over all possibilities. For example, if one hand total has an advantage of positive 5% and another hand has a advantage of -6%, than the total advantage for the two hands is +1%. When the reader understands this game it will be easy to translate the concepts to any other casino game with a static advantage over the player.
Most games of chance reflect the mathematical concept known as “the law of independent trials.” This states that past events have no relevance on future events. This is easily displayed in Roulette and Craps. For example, when a coin is flipped there is a 50% chance that the outcome would be heads and a 50% chance that the outcome would be tails.
If the coin comes up 10 heads in a row the next flip would again have a 50% chance of coming up heads. In blackjack what happens in the past directly affects what happens in the future. Blackjack has memory, and the law of independent trials is not valid.
The percent advantage that the casino has over the player (in blackjack) or vice versa is not static. There are many approaches that one can introduce to keep track of the shifting percentages. The simplest and the one that is least subject to player error is the Hi/Lo counting system. This system assigns values of either: 1, -1 or 0 to the cards. All cards 2-6 are assigned a value of 1 and all cards with a face value of 7, 8 and 9 have a value of 0. All tens, face cards and Aces have a value of -1. As the cards are dealt, the player adds the assigned values of the cards up, the summation of these cards after a round of blackjack is termed the running count.
In a positive running count, the value is normalized into an average of how many more high cards than low cards (or low cards than high cards) there are per deck. To accomplish this, the player estimates how many decks are remaining and, the running count is then divided by how many decks remain, and this value is termed the true count. For example, if a player has observed three decks of a six deck shoe being played, and the running count is a 15, that is fifteen more low cards (2-6) have been played than high cards (10s, face cards and aces) through the first three decks of the shoe; the player then takes the running count (15) and divides by the decks remaining (3), and this would give a true count of 5.
The player subtracts an offset: usually 1, which takes into account the casinos advantage at the start of the deck or shoe (this offset is dependent upon several factors such as the rules of the game and the number of decks used) and that number, is the number of units the player would wager on the next hand. For every whole unit increment (plus or minus) observed in the true count, the player advantage increases by approximately 0.5%, positive or negative, respectively.
When a preponderance of high cards remain, the true count is high and the player has an advantage over the casino. This occurs for three reasons. First, blackjacks are dealt more frequently and, since the payoff on a blackjack is asymmetric (the player gets paid 3:2 on a player blackjack, but only loses his initial bet on a dealer blackjack), this benefits the player. Secondly, some of the players’ options become more valuable, such as splitting and doubling down.
Usually a player would like to see a high card come out when doubling down or splitting, or the player exercises these options when the dealer is weak and a high card will cause the dealer to break (a hit that would cause the dealer to go over 21). These plays have a higher return when the remaining deck is rich in high cards.
Finally, the player may vary their strategy depending upon the composition of the remaining cards. With a preponderance of high cards, the player can stand on more stiff hands (totals of 12-16), double down more often with strong totals (cards equal to 9, 10 or 11) or, when the dealer is weak and susceptible to going over 21, the player may stand. In contrast, the rules prohibit the dealer from varying their strategy. The combination of these factors gives rise to situations where the casinos edge is overcome and a skilled player has an advantage over the house.
1. Bet Size
2. Number of Hands or Spins
3. Percent Advantage
$50=1$ (bet)*0.5% (%advantage)*100(# hands played)
To stick with the coin flip example, variance helps answer the question of whether or not it would it be surprising if we observed 45 heads out of 100 trials, or if we observed only 5 heads in 100 coin flips. The answers are no and yes. Getting only 5 heads in 100 coin flips would virtually prove you were flipping a weighted coin. Understanding this concept is crucial for evaluating casino gaming results, since proper statistical analysis is required in order to determine if the results (good or bad) are a function of luck or skill. It essentially determines whether or not a player or casino is being cheated.
Variance is usually discussed in terms of standard deviations, and that will be the case going forward in this discussion. Standard deviation is equal to the square root of the variance. The standard deviation for a series of trials is represented by the Greek letter σ (sigma) and is equal to the standard deviation of each event multiplied by the square root of the number of events. The mathematical statement reads as:
σ (total)= σ( event)*√(Number of Events)
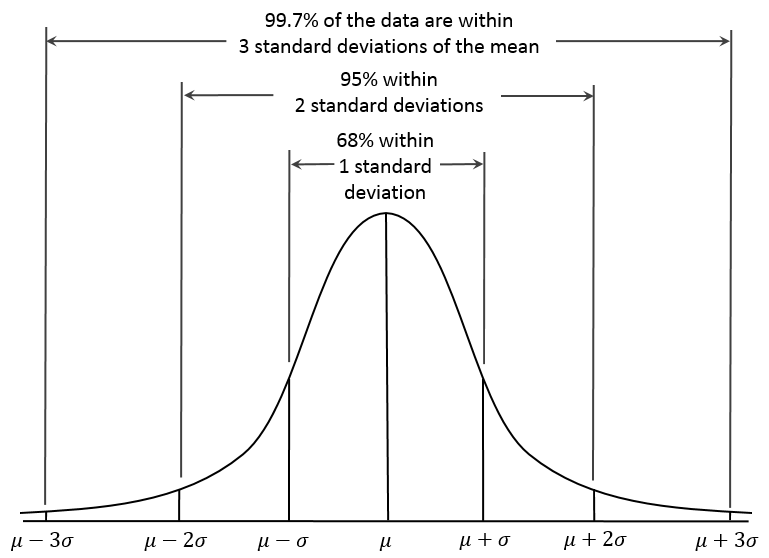
According to the Gaussian distribution curve, there is just over a 68% chance that the result will be within one standard deviation, plus or minus of the expected value. There is a just over a 95% chance that the results will be within two standard deviations, plus or minus of the expected value. There is approximately a 99.9% chance that the results will be within three standard deviations at any given time.
Applying this to the scenario of 100 flips of a coin we conclude that the standard deviation for 100 trials is 10 times (square root of 100) the standard deviation for a single trial (which is 0.5), which yields a standard deviation of 5 for the 100 trial experiment. In the coin flip scenario we expect the 50 of the 100 flips to land on heads and 50 of the 100 to land on tails. Including the standard deviation concept of plus or minus 5, there is a 68% chance that for a 100 flips of a coin the heads side will come up between 45 and 55 times.
There is a 95% probability that the number of heads will be between 40 and 60 (2*σ) and a 99.9% chance that the number of heads will fall between 35 and 65 (3*σ).
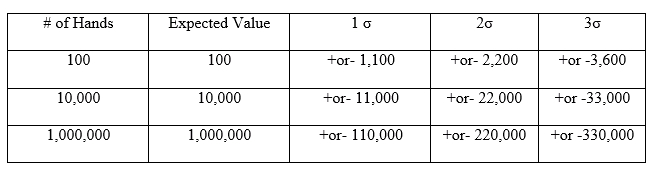
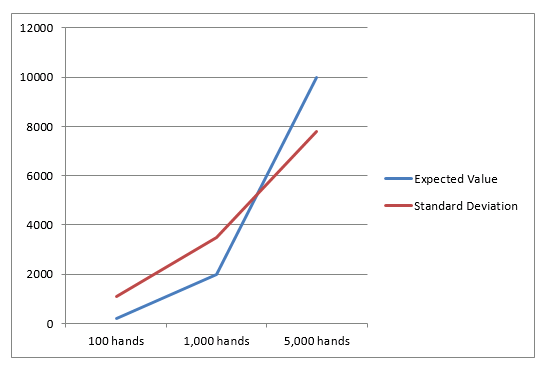
Applying the expected value and standard deviation equations to the betting unit of 100 dollars for a casino game with a 1% advantage over the player the following results are computed.
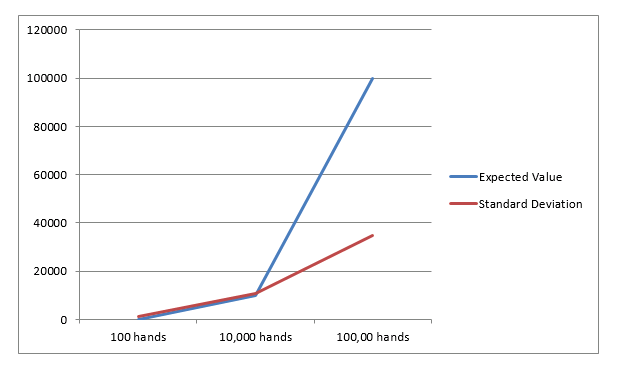
Graphically it is represented as follows.
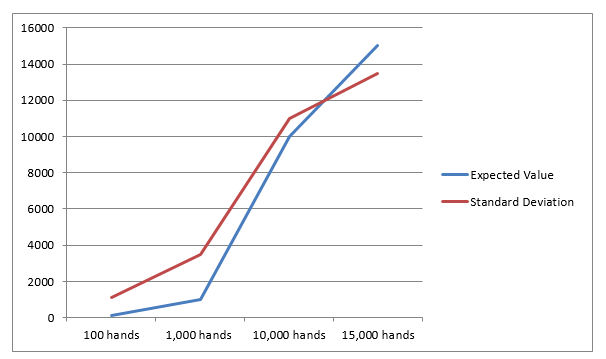
As the number of events increase, the standard deviation gets smaller and smaller relative to the expected value. At some point along the curve the expected value and standard deviations intersect. At this point there is an 84% chance that the standard deviation will be less than the expected value. This means there is an 84% chance that a profit will be made from that point forward and that your funds will never be depleted. This intersection point for a 1% advantage is shown in the following graph.
If 1 million players wager 1 dollar and, one player wins 500K than the casino makes a profit of 500K and an average loss of 50 cents per wager is perceived. In slot machines the advertised pay back is often in the neighborhood of 97-99%. This is over the entire life of the machine where a machine may collect 100s of millions of dollars in action over its lifetime. Table games are slightly different because some include a skill component and the % advantage the casino has varies from player to player. But the same general principle applies.
This article is an in depth analysis of the mathematics of casino gaming. The information presented here is valid for live blackjack play as well as online play. However; the Blackjack software programs that online casinos use include all of the cards in every new round of play. The analysis will apply to the game of Blackjack. Blackjack is a game of dynamic probabilities and shifting percentages. But even though the percents are constantly changing, the cumulative percentage of the overall advantage remains constant.
This is achieved by taking the sum of the advantages over all possibilities. For example, if one hand total has an advantage of positive 5% and another hand has a advantage of -6%, than the total advantage for the two hands is +1%. When the reader understands this game it will be easy to translate the concepts to any other casino game with a static advantage over the player.
GAMING STATISTICS
Understanding the statistics involved in casino gaming is essential in evaluating the results. This assertion is valid for both the player and the casinos. The knowledge presented here is here is required to determine whether the results good or bad, lye in the statistical realm of possibility.Most games of chance reflect the mathematical concept known as “the law of independent trials.” This states that past events have no relevance on future events. This is easily displayed in Roulette and Craps. For example, when a coin is flipped there is a 50% chance that the outcome would be heads and a 50% chance that the outcome would be tails.
If the coin comes up 10 heads in a row the next flip would again have a 50% chance of coming up heads. In blackjack what happens in the past directly affects what happens in the future. Blackjack has memory, and the law of independent trials is not valid.
HOW BLACKJACK IS DIFFERENT ?
In Blackjack each card has a specific value that it adds to, or subtracts from the initial advantage that the casino has over the player. The initial advantage is derived from the rules of the game. When enough of the right cards are dealt, the advantage swings in the players favor. In blackjack when an Ace or 10 value card is dealt the casino advantage over the player increases. When lower value cards are put in play (2-7) the casino advantage decreases, and when enough of those cards are dealt, the player has an advantage over the casino.The percent advantage that the casino has over the player (in blackjack) or vice versa is not static. There are many approaches that one can introduce to keep track of the shifting percentages. The simplest and the one that is least subject to player error is the Hi/Lo counting system. This system assigns values of either: 1, -1 or 0 to the cards. All cards 2-6 are assigned a value of 1 and all cards with a face value of 7, 8 and 9 have a value of 0. All tens, face cards and Aces have a value of -1. As the cards are dealt, the player adds the assigned values of the cards up, the summation of these cards after a round of blackjack is termed the running count.
In a positive running count, the value is normalized into an average of how many more high cards than low cards (or low cards than high cards) there are per deck. To accomplish this, the player estimates how many decks are remaining and, the running count is then divided by how many decks remain, and this value is termed the true count. For example, if a player has observed three decks of a six deck shoe being played, and the running count is a 15, that is fifteen more low cards (2-6) have been played than high cards (10s, face cards and aces) through the first three decks of the shoe; the player then takes the running count (15) and divides by the decks remaining (3), and this would give a true count of 5.
The player subtracts an offset: usually 1, which takes into account the casinos advantage at the start of the deck or shoe (this offset is dependent upon several factors such as the rules of the game and the number of decks used) and that number, is the number of units the player would wager on the next hand. For every whole unit increment (plus or minus) observed in the true count, the player advantage increases by approximately 0.5%, positive or negative, respectively.
When a preponderance of high cards remain, the true count is high and the player has an advantage over the casino. This occurs for three reasons. First, blackjacks are dealt more frequently and, since the payoff on a blackjack is asymmetric (the player gets paid 3:2 on a player blackjack, but only loses his initial bet on a dealer blackjack), this benefits the player. Secondly, some of the players’ options become more valuable, such as splitting and doubling down.
Usually a player would like to see a high card come out when doubling down or splitting, or the player exercises these options when the dealer is weak and a high card will cause the dealer to break (a hit that would cause the dealer to go over 21). These plays have a higher return when the remaining deck is rich in high cards.
Finally, the player may vary their strategy depending upon the composition of the remaining cards. With a preponderance of high cards, the player can stand on more stiff hands (totals of 12-16), double down more often with strong totals (cards equal to 9, 10 or 11) or, when the dealer is weak and susceptible to going over 21, the player may stand. In contrast, the rules prohibit the dealer from varying their strategy. The combination of these factors gives rise to situations where the casinos edge is overcome and a skilled player has an advantage over the house.
CALCULATING THE WIN
To determine what the amount that one expects to win over a given time (either the casino or player), three key pieces of information are required. They are:1. Bet Size
2. Number of Hands or Spins
3. Percent Advantage
IN EQUATION FORM THE STATEMENT READS:
Expected $ win=$bet*%advantage *# hands playedEQUATION 1
If we apply the expected value scenario to a flip of a coin, we know that there are 2 sides to a coin, so there is a 50% chance of landing on heads and a 50% chance of landing on tails. When we bet 1 dollar per flip, the equation for how much we expect to win over 100 flips is:$50=1$ (bet)*0.5% (%advantage)*100(# hands played)
EQUATION 2
In this example we wagered 100 dollars and won 50 dollars on 50 of those bets. We were also able to keep the original bet of $1 on 50 of those 100 bets. Also we lost $1 on 50 of the bets. This leads to a zero sum game. No winners no losers.AM I WHERE I SHOULD BE ?
When a coin is flipped 100 times the outcome is rarely exactly 50 heads and 50 tails. Therefore we must introduce the concept of variance per number of events. Variance is a measure of statistical dispersion. In layman’s terms, it deals with how far away from the expected value the result of a trial or experiment might be.To stick with the coin flip example, variance helps answer the question of whether or not it would it be surprising if we observed 45 heads out of 100 trials, or if we observed only 5 heads in 100 coin flips. The answers are no and yes. Getting only 5 heads in 100 coin flips would virtually prove you were flipping a weighted coin. Understanding this concept is crucial for evaluating casino gaming results, since proper statistical analysis is required in order to determine if the results (good or bad) are a function of luck or skill. It essentially determines whether or not a player or casino is being cheated.
Variance is usually discussed in terms of standard deviations, and that will be the case going forward in this discussion. Standard deviation is equal to the square root of the variance. The standard deviation for a series of trials is represented by the Greek letter σ (sigma) and is equal to the standard deviation of each event multiplied by the square root of the number of events. The mathematical statement reads as:
σ (total)= σ( event)*√(Number of Events)
EQUATION 3
The following figure shows how likely results are to fall within one, two and three standard deviations of the expected result. In the graphical representation the expected value is indicated by the Greek letter µ and the Standard Deviation is represented by the Greek letter σ.According to the Gaussian distribution curve, there is just over a 68% chance that the result will be within one standard deviation, plus or minus of the expected value. There is a just over a 95% chance that the results will be within two standard deviations, plus or minus of the expected value. There is approximately a 99.9% chance that the results will be within three standard deviations at any given time.
Applying this to the scenario of 100 flips of a coin we conclude that the standard deviation for 100 trials is 10 times (square root of 100) the standard deviation for a single trial (which is 0.5), which yields a standard deviation of 5 for the 100 trial experiment. In the coin flip scenario we expect the 50 of the 100 flips to land on heads and 50 of the 100 to land on tails. Including the standard deviation concept of plus or minus 5, there is a 68% chance that for a 100 flips of a coin the heads side will come up between 45 and 55 times.
There is a 95% probability that the number of heads will be between 40 and 60 (2*σ) and a 99.9% chance that the number of heads will fall between 35 and 65 (3*σ).
Applying the expected value and standard deviation equations to the betting unit of 100 dollars for a casino game with a 1% advantage over the player the following results are computed.
Graphically it is represented as follows.
As the number of events increase, the standard deviation gets smaller and smaller relative to the expected value. At some point along the curve the expected value and standard deviations intersect. At this point there is an 84% chance that the standard deviation will be less than the expected value. This means there is an 84% chance that a profit will be made from that point forward and that your funds will never be depleted. This intersection point for a 1% advantage is shown in the following graph.
FOR SIMPLICITY THE STANDARD DEVIATION VALUE IS ABSOLUTE
The intersect point between the expected value and standard deviation is just below 12,000 hands. At 12,000 hands there is an 84% chance that the expected value will surpass the negative standard deviation, indicating the player will not zero out their bankroll 84% of the time. When the overall advantage is increased the “equivalence” point, or the number of hands at which the expected value equals the standard deviation, is reached in fewer hands. Computing the same graph with 2% advantage the graph shows an equivalence point that is substantially lower.
FOR SIMPLICITY THE STANDARD DEVIATION VALUE IS ABSOLUTE
In the final analysis casinos are able to get to the “equivalence” point extremely fast. This makes sense because casinos are playing the game 24 hours a day 7 days a week. And because almost all players play to a disadvantage the casinos makes more and more money with less and less variance relative to their expected value. In forth coming articles I will discuss various aspects of attacking casino games for profit.