Beating Loss Rebate Programs: The Biggest Advantage Play

By Anonymous
|
|
When I heard Don Johnson (DJ) speak at the World Game Protection Conference in 2013, it became clear that DJ was an advantage player playing at the highest level. In performing his act of “social engineering,” DJ negotiated a number of perks that moved the game in his direction, until he had a substantial edge. Foremost among his negotiated perks were liberal blackjack rules (0.263% house edge), a large wager size ($100,000) a substantial loss rebate (20% on losses over $500,000 per day), show up money ($50,000 per day), and the ability to have an entourage at the table with him (to help him Wong-out negative shoes). Together, these perks allowed DJ to have an expected value of about $137,000 per day. Not too shabby.
The most significant insight I got from DJ was that his was not a singular occurrence. DJ showed that with the right type of personality and bankroll, the AP could profitably target high-level loss rebate programs. All that would be required is a loss rebate that is based on total losses and not on time played. With a large enough rebate percentage, win/loss thresholds can be developed that optimize revenue for the AP. This is a big play, certainly the biggest ongoing advantage play I know about.
Most casino marketing books preach the need to have loss rebate percentages rely on time played. They can’t simply be based on the total amount lost by the player. For example, in baccarat, the casino may offer a loss rebate of 5% for playing 1-to-9 shoes, 10% for 11-to-19 shoes, and 15% for 20 shoes or more on a single trip. This percentage will apply to any player loss, there does not need to be a threshold minimum loss. This type of graduated schedule forces the player to earn his rebate, thereby generating sufficient theoretical win for the casino to pay for his loss rebate.
More typical, though, is for a casino to offer rebates that are loss-based and not time-based. For example, a casino might offer a 5% loss rebate for a loss from $100,000 to $300,000, a 10% loss rebate for a loss from $300,000 to $500,000 and a 15% loss rebate for any losses over $500,000. This type of loss rebate program encourages hit-and-run play. Bet as big as possible on as high-variance/low-edge game as possible. If the player loses big, then he cashes out his rebate and heads to the next casino where he can get a similar deal. If the player wins big, he cashes out his winnings and heads to the next casino where he can get a similar deal. DJ negotiated exactly this framework.
The typical player has three thresholds to stop playing. He can:
The AP who is attempting to take advantage of a loss rebate program will stop playing exclusively based on his win/loss thresholds and not based on a time threshold. There are optimal values for the win/loss thresholds that maximize the AP’s expected income for a single trip to a casino. The AP should keep playing until he hits one of those two stopping points (if possible), and then quit playing until the next “trip.” In the case of DJ, his trip reset every day. For a more typical player, the trip resets based on a physical trip to a casino that is negotiated along with airfare and other perks. It is up to the casino’s marketing department to define a “trip” for a high-level player.
In an attempt to understand the value of the loss rebate program to an AP, I ran a bunch of simulations. These simulations all assumed that the AP was playing the same variation of blackjack that DJ played (S17, DOA, DAS, RSA, LSR) with house edge 0.263%. I assumed the AP had a bankroll of $1,000,000 dollars. I assumed that for some level of loss, the AP would be given a loss rebate. I then considered wagers for the AP of sizes $50,000 and $100,000 and loss rebate percentages of 10%, 13%, 15%, 18% and 20%. In each case, I determined the optimal win threshold for the AP to maximize his dollar-win per trip. Obviously, the bankroll and bet size can be scaled: the simulations are for bankrolls equal to 10 bets and 20 bets respectively.
In my model, the AP is going to play until he either crosses his win threshold, or doesn’t have enough money to make another bet. Specifically, if the AP”s bet size was $50,000, then I required the AP to have at least $100,000 left (he may need to double or split). If the AP’s bet size was $100,000, then I required the AP to have at least $200,000 left. So, the loss thresholds were a loss of $900,001 for a $50,000 bet and a loss of $800,001 for a $100,000 bet.
Note that the specific amount of loss at which the AP triggers his loss rebate doesn’t matter to my simulations. In my model, the AP will always get the maximum rebate on his losses if he leaves a loser. Remember, he’s playing until he wins a lot or goes broke (not enough money to complete another bet, including a split or double). Don Johnson didn’t leave when he lost $500,000, even though that was the point that triggered his 20% rebate. He kept playing past that point, using a threshold loss of more than $800,000 to quit. It’s the same thing in my simulations.
My methodology was to crunch a lot of players in a massive simulation. For each loss rebate percent and wager size and win threshold, I simulated twenty million (20,000,000) “Don Johnson”-like players. I then averaged their results to get the overall estimates for their edge, average hands played, average loss rebate and average win. I did this for various win thresholds. I then determined the optimal win threshold by choosing the win threshold that gave the largest “average win” for the AP. The “quit point” in the tables gives that optimal win threshold.
The quit point is the bankroll size at which the AP should quit playing for the trip. This quit point includes the AP’s initial bankroll. The AP can do no better in the long run than to quit playing when his bankroll equals or exceeds this amount, or when he hits his loss threshold.
Here are the results of my simulations:
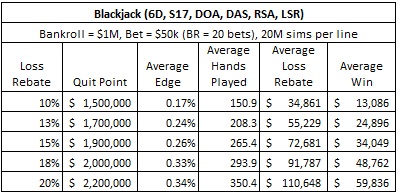
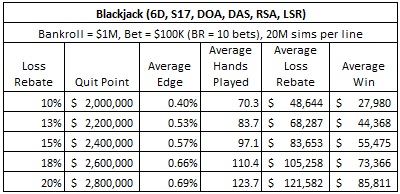
Even with a 10% rebate on losses and a $50,000 maximum bet, the AP can get the edge over the house just by exploiting the rebate program. By quitting when he has either lost $900,001 or has won $500,000 (total bankroll = $1,500,000), his long-term average will be a win of about $13,000 per day. This AP is no-doubt getting many other perks for his play, putting the casino squarely in the red.
Maybe this type of opportunity is what led one message board author to write this post, asking his compatriots to not discuss this topic in a venue where others might take notice:
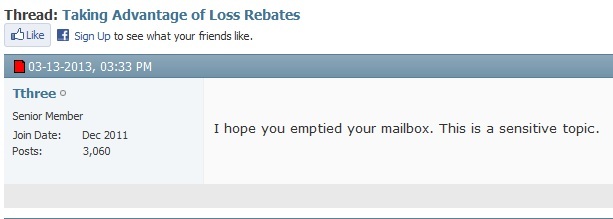
It’s obvious the system is broken and that it’s been broken for a long time. This fracture is systemic. Any action to fix a casino's internal discount procedures may jeopardize their entire high-end play. A valuable player does not want new obstacles put in the way of benefits he has been receiving all along. He’ll gladly defect to another casino where the loss rebate system operates in the manner he is accustomed. Competitors will fall over backwards to provide this to him. It is going to take a revolution in the industry to eliminate this type of advantage play. In the mean time, the best casinos can do is to identify high-level players who are beating their discount programs and back them off.
The most significant insight I got from DJ was that his was not a singular occurrence. DJ showed that with the right type of personality and bankroll, the AP could profitably target high-level loss rebate programs. All that would be required is a loss rebate that is based on total losses and not on time played. With a large enough rebate percentage, win/loss thresholds can be developed that optimize revenue for the AP. This is a big play, certainly the biggest ongoing advantage play I know about.
Most casino marketing books preach the need to have loss rebate percentages rely on time played. They can’t simply be based on the total amount lost by the player. For example, in baccarat, the casino may offer a loss rebate of 5% for playing 1-to-9 shoes, 10% for 11-to-19 shoes, and 15% for 20 shoes or more on a single trip. This percentage will apply to any player loss, there does not need to be a threshold minimum loss. This type of graduated schedule forces the player to earn his rebate, thereby generating sufficient theoretical win for the casino to pay for his loss rebate.
More typical, though, is for a casino to offer rebates that are loss-based and not time-based. For example, a casino might offer a 5% loss rebate for a loss from $100,000 to $300,000, a 10% loss rebate for a loss from $300,000 to $500,000 and a 15% loss rebate for any losses over $500,000. This type of loss rebate program encourages hit-and-run play. Bet as big as possible on as high-variance/low-edge game as possible. If the player loses big, then he cashes out his rebate and heads to the next casino where he can get a similar deal. If the player wins big, he cashes out his winnings and heads to the next casino where he can get a similar deal. DJ negotiated exactly this framework.
The typical player has three thresholds to stop playing. He can:
- Exhaust his bankroll (loss threshold).
- Win a sufficient amount so that he feels like quitting (win threshold).
- Exhaust his time bank (time threshold).
The AP who is attempting to take advantage of a loss rebate program will stop playing exclusively based on his win/loss thresholds and not based on a time threshold. There are optimal values for the win/loss thresholds that maximize the AP’s expected income for a single trip to a casino. The AP should keep playing until he hits one of those two stopping points (if possible), and then quit playing until the next “trip.” In the case of DJ, his trip reset every day. For a more typical player, the trip resets based on a physical trip to a casino that is negotiated along with airfare and other perks. It is up to the casino’s marketing department to define a “trip” for a high-level player.
In an attempt to understand the value of the loss rebate program to an AP, I ran a bunch of simulations. These simulations all assumed that the AP was playing the same variation of blackjack that DJ played (S17, DOA, DAS, RSA, LSR) with house edge 0.263%. I assumed the AP had a bankroll of $1,000,000 dollars. I assumed that for some level of loss, the AP would be given a loss rebate. I then considered wagers for the AP of sizes $50,000 and $100,000 and loss rebate percentages of 10%, 13%, 15%, 18% and 20%. In each case, I determined the optimal win threshold for the AP to maximize his dollar-win per trip. Obviously, the bankroll and bet size can be scaled: the simulations are for bankrolls equal to 10 bets and 20 bets respectively.
In my model, the AP is going to play until he either crosses his win threshold, or doesn’t have enough money to make another bet. Specifically, if the AP”s bet size was $50,000, then I required the AP to have at least $100,000 left (he may need to double or split). If the AP’s bet size was $100,000, then I required the AP to have at least $200,000 left. So, the loss thresholds were a loss of $900,001 for a $50,000 bet and a loss of $800,001 for a $100,000 bet.
Note that the specific amount of loss at which the AP triggers his loss rebate doesn’t matter to my simulations. In my model, the AP will always get the maximum rebate on his losses if he leaves a loser. Remember, he’s playing until he wins a lot or goes broke (not enough money to complete another bet, including a split or double). Don Johnson didn’t leave when he lost $500,000, even though that was the point that triggered his 20% rebate. He kept playing past that point, using a threshold loss of more than $800,000 to quit. It’s the same thing in my simulations.
My methodology was to crunch a lot of players in a massive simulation. For each loss rebate percent and wager size and win threshold, I simulated twenty million (20,000,000) “Don Johnson”-like players. I then averaged their results to get the overall estimates for their edge, average hands played, average loss rebate and average win. I did this for various win thresholds. I then determined the optimal win threshold by choosing the win threshold that gave the largest “average win” for the AP. The “quit point” in the tables gives that optimal win threshold.
The quit point is the bankroll size at which the AP should quit playing for the trip. This quit point includes the AP’s initial bankroll. The AP can do no better in the long run than to quit playing when his bankroll equals or exceeds this amount, or when he hits his loss threshold.
Here are the results of my simulations:


Even with a 10% rebate on losses and a $50,000 maximum bet, the AP can get the edge over the house just by exploiting the rebate program. By quitting when he has either lost $900,001 or has won $500,000 (total bankroll = $1,500,000), his long-term average will be a win of about $13,000 per day. This AP is no-doubt getting many other perks for his play, putting the casino squarely in the red.
Maybe this type of opportunity is what led one message board author to write this post, asking his compatriots to not discuss this topic in a venue where others might take notice:

It’s obvious the system is broken and that it’s been broken for a long time. This fracture is systemic. Any action to fix a casino's internal discount procedures may jeopardize their entire high-end play. A valuable player does not want new obstacles put in the way of benefits he has been receiving all along. He’ll gladly defect to another casino where the loss rebate system operates in the manner he is accustomed. Competitors will fall over backwards to provide this to him. It is going to take a revolution in the industry to eliminate this type of advantage play. In the mean time, the best casinos can do is to identify high-level players who are beating their discount programs and back them off.


