The Challenges of Match Play

By Anonymous
|
|
Match play has been around for years as a staple of marketing used to attract table game play. Nevertheless, there are still a number of misunderstandings and misconceptions about its value, its use, and its vulnerabilities. In light of the explosion of free play for slots, there is pressure to issue more match play to keep up. Just as determining the cost of free play is a challenge, match play coupons are also a source of complicated and important questions.
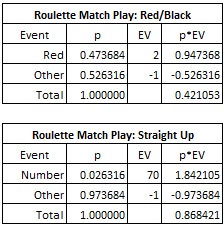
Consider a $100 match play coupon that a player can use on any table game. If this player uses his coupon to make a red/black wager on roulette (house edge = 5.26%), then the coupon is worth $42.11 to the player. However, if the player can use this $100 match play wager to wager on a number straight up, then that same coupon is worth $86.84. A $100 match play coupon is worth 106% more when played on a number straight-up in roulette then when it is played on an even-money bet. The cost more than doubles!
Here is the combinatorial analysis showing the computation of match play value for roulette:
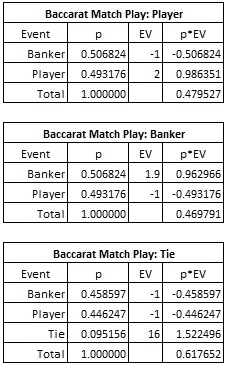
A similar situation occurs in baccarat. If a $100 match play coupon is used on the Player wager and left there until it resolves, it is worth $47.95. If it is used on the Banker wager, it is worth $46.98. But if it can be used on the Tie bet that pays 8-to-1, that same $100 coupon is worth $61.77. Even though the Tie bet has a huge house edge (14.36%), the coupon is still worth 31% more to the player when used on the Tie bet than if used to make a Banker bet.
Here is the combinatorial analysis showing the computation of match play value for baccarat:
The value of a match play coupon depends both on the house edge of the wager and volatility of the wager. A higher house edge decreases the cost of the coupon. Higher volatility usually increases the cost, as the roulette and baccarat examples show. For this reason, match play coupons should be restricted to even-money bets only. But, curiously, volatility of the wager doesn’t always come at a cost.
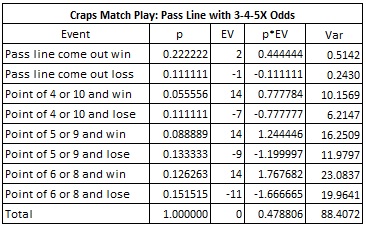
The value of a $100 match play coupon placed on the pass line in craps is worth $47.88. There is a policy question each casino must answer about the use of a match play coupon in craps. Can the player place an odds bet based on the total value (including his match play) or just the cash part that he used to match the coupon? Whatever the casino’s policy about odds bets and match play, the value of the coupon doesn’t change. However, the volatility changes substantially; for example, if 3x/4x/5x odds are offered, then allowing full odds on the wager, including the match play, has the same volatility as offering odds of 6x/8x/10x on the cash part of the wager.
Here is the combinatorial analysis showing the computation of match play value for a player making a pass line wager. In particular, note the standard deviation (square root of variance) is 9.4025. This degree of volatility is usually reserved for slot machines -- in this case, the casino is playing the slot.
On blackjack, the use of free play can become very complicated. Can the player double down on the whole value including the coupon, or just on the cash part? What about splits? For surrender, does the player get half the value of the coupon back? Can insurance or “even money” be taken on the coupon as well as the cash? The guidelines for using match play coupons on blackjack are often not completely spelled out. In valuing the coupon, the specific rules of the blackjack game also come into play, along with the strength of the player.
Like any business, casinos should seek to maximize profit while minimizing risk. In the case of match play coupons, maximizing profit means limiting their use to even-money bets only. Minimizing risk means not allowing players to take odds on coupons in craps. But minimizing risk is often completely misunderstood when the question becomes offsetting coupons.
A common issue raised by table games management is the use of match play coupons in a way that gives the casino no shot at the player’s money. The most frequent way this happens is when, in baccarat, a couple uses two coupons to make a Banker wager and a Player wager simultaneously, making them guaranteed winners.
For example, suppose a couple is given two $100 match play coupons that are wagered on the Player and Banker on a single hand in baccarat. If the result is that the Player wagers wins, then the couple has won a net of $100. If the Banker wager wins, then the couple has won a net of $90. If the result is a Tie, then the coupons can be used again. Taking into account the difference in probability that the Player coupon will win or Banker coupon will win, the average win for the couple is $94.93.
How is this different from allowing this couple to use these two coupons on two successive hands rather than on the same hand? One person plays the $100 coupon on Player until it is resolved. Then the other person plays the $100 coupon on Banker until it is resolved. As we saw above, the value of a coupon if used on the Player side is $47.95 and the value is $46.98 if used on the Banker side. Sure enough, $47.95 + $46.98 = $94.93, giving the same theoretical value for these coupons.
The argument is a bit tricky when management complains that the house can’t win both bets. As a casino, there is a feeling that there should be no “free” wagers. When coupons are used to offset each other, the casino winning both wagers is rendered impossible. But what is overlooked in this argument is that it’s also true that the casino losing both wagers is rendered impossible. In other words, the volatility is greatly reduced when the coupons offset each other. Viewed in this way, the casino should welcome using coupons in this manner. Lowering volatility reduces risk and is always the preferred choice for any fixed expense.
Finally, it’s always important to keep in mind that there are individuals who are dedicated to using coupons purely for their cash value and nothing more. Many casinos have learned this lesson the hard way.
A few years ago, for example, a casino included a $25 match play coupon in the Sunday issue of a newspaper. An AP called the newspaper and special ordered 1000 copies to be delivered to his home. He then hired help to patiently cut out the coupons from each paper. Because no restrictions were placed on the use or transfer of these coupons, he was able to use more than one hundred himself, while selling the rest to other advantage players.
In another case, a casino published a $5000 match play coupon in a local magazine. The coupon stated that it could be used for any amount up to $5000. The marketing idea was that this promotion would draw new players into the casino to use the coupon at whatever denomination the player could afford. In other words, it was a “catch-all” match play coupon. The casino expected the bulk of these coupons to be used at the $5, $10 or $25 level by real players. However, when advantage players started showing up in droves, playing the full $5000 value, the casino learned a tough lesson.
There is no end to the variety of ways casinos find to lose money to advantage players through their match play coupons. For example, a casino in Las Vegas had a sign-up bonus coupon sheet that included various coupons that totaled $500 in match play. When advantage players discovered the opportunity, they rounded up people off the street and paid them a flat fee to get these sheets, play them, and return the cash profit (if any) to the advantage players.
As the use of match play as a marketing tool continues to expand, it is vitally important that its value, its use and its vulnerabilities be clearly understood. Marketing needs to know its value, volatility and risk across all permitted wagering opportunities. Table games needs to know the precise details of its use. And everyone involved in protecting the casino’s bottom line needs to know its vulnerabilities. The new wave of match play coupons deserves the casino’s full attention.
Consider a $100 match play coupon that a player can use on any table game. If this player uses his coupon to make a red/black wager on roulette (house edge = 5.26%), then the coupon is worth $42.11 to the player. However, if the player can use this $100 match play wager to wager on a number straight up, then that same coupon is worth $86.84. A $100 match play coupon is worth 106% more when played on a number straight-up in roulette then when it is played on an even-money bet. The cost more than doubles!
Here is the combinatorial analysis showing the computation of match play value for roulette:

A similar situation occurs in baccarat. If a $100 match play coupon is used on the Player wager and left there until it resolves, it is worth $47.95. If it is used on the Banker wager, it is worth $46.98. But if it can be used on the Tie bet that pays 8-to-1, that same $100 coupon is worth $61.77. Even though the Tie bet has a huge house edge (14.36%), the coupon is still worth 31% more to the player when used on the Tie bet than if used to make a Banker bet.
Here is the combinatorial analysis showing the computation of match play value for baccarat:

The value of a match play coupon depends both on the house edge of the wager and volatility of the wager. A higher house edge decreases the cost of the coupon. Higher volatility usually increases the cost, as the roulette and baccarat examples show. For this reason, match play coupons should be restricted to even-money bets only. But, curiously, volatility of the wager doesn’t always come at a cost.
The value of a $100 match play coupon placed on the pass line in craps is worth $47.88. There is a policy question each casino must answer about the use of a match play coupon in craps. Can the player place an odds bet based on the total value (including his match play) or just the cash part that he used to match the coupon? Whatever the casino’s policy about odds bets and match play, the value of the coupon doesn’t change. However, the volatility changes substantially; for example, if 3x/4x/5x odds are offered, then allowing full odds on the wager, including the match play, has the same volatility as offering odds of 6x/8x/10x on the cash part of the wager.
Here is the combinatorial analysis showing the computation of match play value for a player making a pass line wager. In particular, note the standard deviation (square root of variance) is 9.4025. This degree of volatility is usually reserved for slot machines -- in this case, the casino is playing the slot.

On blackjack, the use of free play can become very complicated. Can the player double down on the whole value including the coupon, or just on the cash part? What about splits? For surrender, does the player get half the value of the coupon back? Can insurance or “even money” be taken on the coupon as well as the cash? The guidelines for using match play coupons on blackjack are often not completely spelled out. In valuing the coupon, the specific rules of the blackjack game also come into play, along with the strength of the player.
Like any business, casinos should seek to maximize profit while minimizing risk. In the case of match play coupons, maximizing profit means limiting their use to even-money bets only. Minimizing risk means not allowing players to take odds on coupons in craps. But minimizing risk is often completely misunderstood when the question becomes offsetting coupons.
A common issue raised by table games management is the use of match play coupons in a way that gives the casino no shot at the player’s money. The most frequent way this happens is when, in baccarat, a couple uses two coupons to make a Banker wager and a Player wager simultaneously, making them guaranteed winners.
For example, suppose a couple is given two $100 match play coupons that are wagered on the Player and Banker on a single hand in baccarat. If the result is that the Player wagers wins, then the couple has won a net of $100. If the Banker wager wins, then the couple has won a net of $90. If the result is a Tie, then the coupons can be used again. Taking into account the difference in probability that the Player coupon will win or Banker coupon will win, the average win for the couple is $94.93.
How is this different from allowing this couple to use these two coupons on two successive hands rather than on the same hand? One person plays the $100 coupon on Player until it is resolved. Then the other person plays the $100 coupon on Banker until it is resolved. As we saw above, the value of a coupon if used on the Player side is $47.95 and the value is $46.98 if used on the Banker side. Sure enough, $47.95 + $46.98 = $94.93, giving the same theoretical value for these coupons.
The argument is a bit tricky when management complains that the house can’t win both bets. As a casino, there is a feeling that there should be no “free” wagers. When coupons are used to offset each other, the casino winning both wagers is rendered impossible. But what is overlooked in this argument is that it’s also true that the casino losing both wagers is rendered impossible. In other words, the volatility is greatly reduced when the coupons offset each other. Viewed in this way, the casino should welcome using coupons in this manner. Lowering volatility reduces risk and is always the preferred choice for any fixed expense.
Finally, it’s always important to keep in mind that there are individuals who are dedicated to using coupons purely for their cash value and nothing more. Many casinos have learned this lesson the hard way.
A few years ago, for example, a casino included a $25 match play coupon in the Sunday issue of a newspaper. An AP called the newspaper and special ordered 1000 copies to be delivered to his home. He then hired help to patiently cut out the coupons from each paper. Because no restrictions were placed on the use or transfer of these coupons, he was able to use more than one hundred himself, while selling the rest to other advantage players.
In another case, a casino published a $5000 match play coupon in a local magazine. The coupon stated that it could be used for any amount up to $5000. The marketing idea was that this promotion would draw new players into the casino to use the coupon at whatever denomination the player could afford. In other words, it was a “catch-all” match play coupon. The casino expected the bulk of these coupons to be used at the $5, $10 or $25 level by real players. However, when advantage players started showing up in droves, playing the full $5000 value, the casino learned a tough lesson.
There is no end to the variety of ways casinos find to lose money to advantage players through their match play coupons. For example, a casino in Las Vegas had a sign-up bonus coupon sheet that included various coupons that totaled $500 in match play. When advantage players discovered the opportunity, they rounded up people off the street and paid them a flat fee to get these sheets, play them, and return the cash profit (if any) to the advantage players.
As the use of match play as a marketing tool continues to expand, it is vitally important that its value, its use and its vulnerabilities be clearly understood. Marketing needs to know its value, volatility and risk across all permitted wagering opportunities. Table games needs to know the precise details of its use. And everyone involved in protecting the casino’s bottom line needs to know its vulnerabilities. The new wave of match play coupons deserves the casino’s full attention.


