Three Card Poker Hole-Card Play: Update #1

Hole-carding 3CP was one of the first advanced plays I was involved with. Back in 2002, when I saw a dealer flash her hole-card in 3CP at my local casino, I was excited and quickly computed optimal strategy and the edge. I thought this was a one-off, that I would not see 3CP hole-cards anywhere else. Imagine my surprise and delight when I went to Las Vegas and saw dealers flashing their hole-cards in casinos everywhere.

 

Back then, nearly every casino used an Ace shuffler. Casinos, and the industry in general, didn't take 3CP seriously as a game protection problem.  The picture below is an example of an Ace shuffler on a 3CP table. Can you imagine how hard it would be to *not* expose a hole-card here?

 

 

Those days are long gone, but hole-carding opportunities for 3CP still exist everywhere

 

As I've pointed out several times in this blog (see this post and this post), hole-carding 3CP has dashed many APs against its rocky shores (including me); it is tough for an AP to beat the game in practice. Errors in reading cards, playing poor games and using cover can evaporate any profit. Most top APs will only play against 3CP when conditions at the game are perfect and there is no better opportunity available.

 

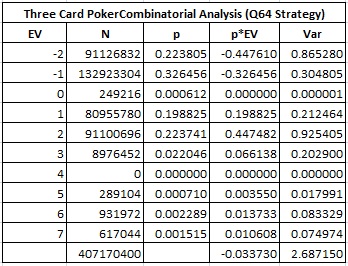
Here is the combinatorial analysis for the main game of 3CP, without seeing any hole-cards. Basic strategy for the main game is to play Q64 or higher and fold all other hands.

 

In particular,

 

• The house edge is 3.3730%.

• The hit frequency (winning 1 or more units) is 44.9127%.

• The standard deviation is 1.6393.

• The modal (most common) outcome is to lose 1 unit.

 

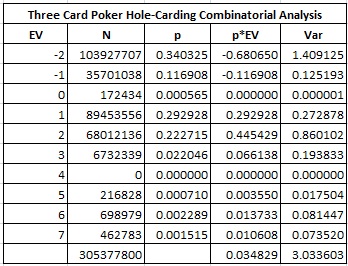
Here is the combinatorial analysis if the player sees one dealer hole-card before making his Play/Fold decision:

 

 

In particular,

 

• The AP's edge is 3.4829%.

• The hit frequency (winning 1 or more units) is 54.2203%.

• The standard deviation is 1.7417.

• The modal (most common) outcome is to lose 2 units.

• The DI (desirability index) is 19.9966.

 

The following spreadsheet contains the analysis for the Play/Fold decision for every starting situation  consisting of three player cards and one dealer hole-card. This spreadsheet only gives dealer hole-cards that are clubs, as permutations of these hands cover every starting hand. Even in this case, there are 270725 starting situations. As far as I can tell, the statistical information contained in this spreadsheet is new to the existing literature on 3CP (including Beyond Counting):

 

TCP_Hole_Card

 

Imagine if I asked you to create a computer-perfect hole-card strategy by combing this spread sheet. Wouldn't that seem like a daunting task? Fortunately for the AP, the answer is trivial. Optimal hole-card strategy is "Any, Q92, K92, A92."

 

The following table gives the AP's edge by dealer hole-card,

 

 

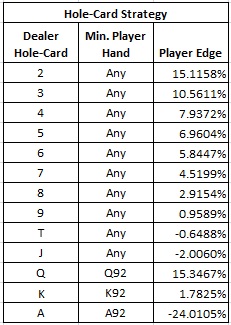
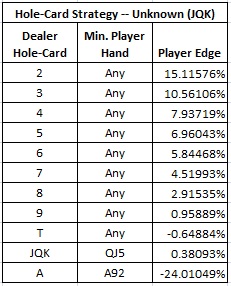
The most common partial-read the hole-card player gets is when the AP sees that the card is a paint card (Jack, Queen, King) but can't otherwise distinguish which paint card it is. In other words, the AP can tell if the card is either 2-T, JQK, or A. Clearly if the AP sees that the card is 2-T, he should always make a Play bet. If the AP sees that the hole-card is an Ace, he should only raise with A92 or better. But what about JQK?

 

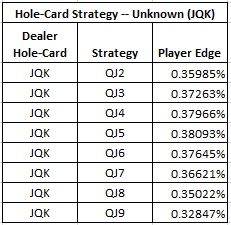
As the following table shows, if the AP sees that the hole-card is an unknown paint card (JQK) then he should make a Play bet with QJ5 or better:

 

 

With the QJ5 strategy, the following table gives the combinatorial analysis for hole-card play when the AP can't distinguish paint cards:

 

 

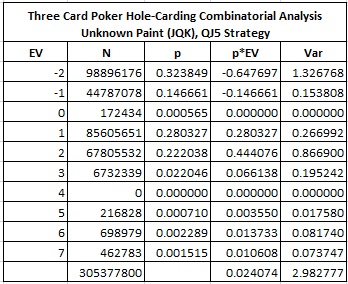
In particular,

 

• The AP's edge is 2.4074%.

• The hit frequency (winning 1 or more units) is 52.8926%.

• The standard deviation is 1.7271.

• The modal (most common) outcome is to lose 2 units.

• The DI (desirability index) is 13.9395.

 

The following table gives the AP's edge based on the observed dealer hole-card when the AP can't distinguished paint cards:

 

 

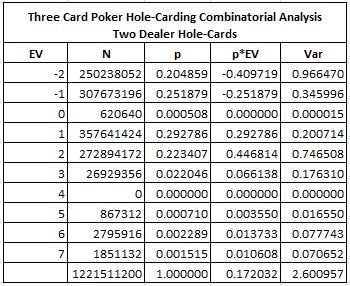
The following table gives the combinatorial analysis in the case the AP sees two dealer hole-cards. This table shows a player edge of 17.2032%.

 

 

I recall many years ago sitting at a table where 3CP was being hand dealt. This was at a strip casino in Las Vegas that had obviously been hit by hole-carders taking advantage of the issues with Ace shufflers. There was a downside to this game protection strategy. A sloppy dealer was exposing all three of her cards. The strategy is pretty easy in this case. You should be able to figure it out yourself. In particular, the AP will never lose 2 units.

 

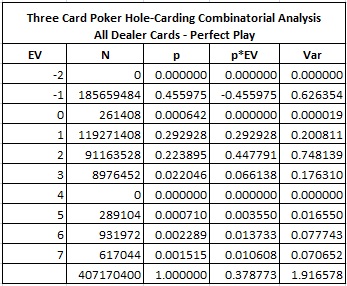
The following table shows a player edge of 37.8733% when the dealer exposes all three of her hole-cards:

 

 

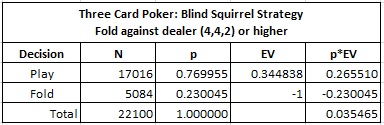
One last thing. Suppose the AP happens to see all three dealer cards before he looks at his own cards. It turns out the AP can still beat 3CP outright and get a 3.5465% edge over the house if the AP folds whenever the dealer has a pair of 4's or higher, otherwise the AP makes a Play bet if the dealer has (3,3,A) or lower.

 

The following spread sheet gives the value of the Play EV for every dealer hand. I sorted it by the strength of the dealer's hand (that's what the "hash" column does) so you can see the strategy break points and other interesting statistics.

 

TCP_EV_By_Dealer_Hand

 

A strategy where an AP can beat the house without looking at his own cards is often referred to as a "Blind Squirrel" strategy. Here is a summary of the results for using the (4,4,2) Blind Squirrel strategy against 3CP:

 

 

If an inspired reader, on either side of the table, wants to learn how to analyze and program hole-carding opportunities, I recommend 3CP as a good starting problem. It is just tough enough to require some careful thought, but it is easy enough that you can figure it out yourself. Moreover, you can write your program in VBA and still have the cycle run in a relatively brief period of time (cycle length = 1,221,511,200, which can be reduced to 305,377,800 if you only consider clubs for the hole-card). 3CP was my first game (way back in 2002). Use the numbers presented here to give it a try.