Beating the 21+3 Blackjack Side Bet, Update #1

The 21 + 3 (TP3) blackjack side bet is based on examining the player’s two cards and the dealer’s up-card. If the three cards form a flush, straight, three-of-a-kind or straight flush, the player wins. The payout for a winning TP3 wager is a flat 9-to-1 and the game has a modest house edge of 3.239%. Recently, several casino sources expressed concern about advantage play against TP3.  I then saw the following post on a web site frequented by APs,  Norm Wattenberger's Blackjacktheforum.com

This was enough to inspire me to go back and have a second look. I decided to run a “perfect play” analysis of TP3 to see if these concerns had merit. Perfect play analysis involves the following steps for a six-deck shoe:

• Go through a shoe one hand at a time.
• Before each hand, compute the exact edge for TP3 based on the cards remaining in the shoe.
• Only make the TP3 wager when the player has the edge, and at no other time.
• Record what happened.

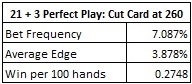
By simulating a bunch of shoes, I was able to get results that give an absolute upper bound for beating TP3 using a method where the player does not have any prior information about the shoe (e.g shuffle tracking). I ran 10,000 shoes and got the following results for perfect play, with the cut card placed at 260 cards (one deck from the end of the shoe):

It is interesting to break this down by the particular location in the shoe a wager is made. The following table gives perfect play statistics by the position in the shoe at which the first card of the hand is dealt:

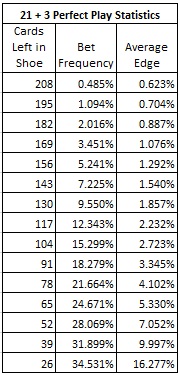
For example, half-way through the shoe (156 cards), the AP will have the edge on 5.241% of the hands at that point, and his average edge when he makes a TP3 wager is 1.292%. If the shoe is dealt deeply, then with 39 cards remaining, the AP will have the edge 31.899% of the time, and his average edge is 9.997%.

What is important to remember is that these are “perfect play” results. The only way to achieve these numbers in a casino would be to use a computer application, live and in real-time, at the table.  It is unreasonable to expect that a player would consider cheating (using a device) for a profit of 0.2748 units per shoe, especially given the low denomination of wagers usually played, and the practical difficulties involved in developing and using such a device. It is, nevertheless, important to consider this possibility in light of the recent attack on the baccarat Lucky Pairs using a device, as discussed in this post.

It is worthwhile to consider how well a human-feasible card counting method fares compared to perfect play. I previously wrote about card counting TP3 in this post.  In that post, I described an approach to counting TP3 using the “suit count.” A team of counters keeps track of the suits. The counters then consider the difference between the most abundant and least abundant suits. This difference is then converted to a true count, and if that count is sufficiently large, the AP has the advantage.

Here are the results of a simulation of one hundred million (100,000,000) six-deck shoes, dealt to 260 cards (52 cards remaining), using the suit count against TP3:

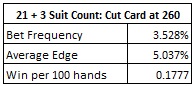
The suit count returns 0.1777 units per 100 hands, compared to a computer perfect return of 0.2748 units per 100 hands.  From these numbers, it is clear that the suit count is highly inefficient, gaining only 64.7% of the potential income from perfect play.  However, even if a perfect card counting system could be developed (it can’t), the best it could do is 0.2748 units per 100 hands. In a worst case scenario, TP3 has a minimal vulnerability to card counting.

It is important to keep an open mind about advantage play. I am very thankful to those who asked the question for inspiring this additional work on TP3. The easy road is to make conclusions based on insufficient information. It’s also the dangerous road. As Confucius said:

Learning without thought is labor lost; thought without learning is perilous.