Card Counting Baccarat Insurance: Natural 9

Baccarat insurance is a side bet that players can make during the play of a hand of baccarat. This side bet is really an aggregate of sides bets, some of which can be made based on the first two cards exposed, and some of which can be made later during the play of the hand. Each of these side bets has its own separate wagering rules and payout. Michael Shackleford determined the house edge for the various insurance wagers in this article. I confess to finding it challenging, based on what Shackleford wrote, to understand how all these opportunities actually arise at the table. I collected documents from various casinos that give pay tables for their insurance bets, but these documents provide little other explanation. A Google search was equally thin in helping me get the big picture. Perhaps if I saw insurance played live, with someone standing beside me explaining it, I might better understand its full scope.

 

I believe I do understand two-card insurance. As baccarat is played in Asia, the player who makes the largest wager at the table gets the opportunity to look at the two cards for the side he wagered on before there is any other action.  If the largest wager is on the Player side, then the first two Player cards are exposed before the two Banker cards. If the largest wager is on Banker, then the first two Banker cards are exposed before the two Player cards. Because of this, it is possible to insure the first hand exposed against the value of the other hand. In particular, natural 8’s and 9’s can be insured. There are additional insurance wagers based on the first two cards, and there is also secondary insurance that can sometimes be taken later in the hand.

 

I asked an expert about betting limitations on insurance. For example, in blackjack, insurance can only be taken by the person making the bet, and insurance is limited to one-half the wager on the main bet.  Are there any similar limitations for baccarat insurance?

 

Here are the questions I asked:

• Can a player insure other people’s Player/Banker bets?
• Can a player only make insurance bets and not otherwise be playing the main game?
• How are betting limits for Insurance wagers determined?

 

Here was the response from the expert:

Technically you have to make a bet before you insurance bet. However, it does not really work in practice because as long as there is a bet, then insurance can be taken. The insurance, at least in the casino I was working for, could not exceed the table maximum or the total amount of bets at any given time. We were struggling with illegal insurance takers all the time. Also having a private laugh when some mark was complaining that he has insured his bet, and paid the money, but the guy who was supposed to pay 9-to-1 just disappeared.

 

What a mess.

 

There is one particular insurance opportunity that I fully understand. It also has the lowest house edge to overcome and is obviously countable. This wager is taking insurance on a natural 9 (INS9).  If the first two cards exposed are a natural 9, then Insurance can be taken that the other hand is a natural 9. This bet pays 9-to-1 if the other hand in also a natural 9, otherwise INS9 loses. At its core, INS9 is simply a side bet that an unknown hand will be a natural 9. The limitation is that this side bet can only be taken when the first hand exposed is a natural 9.

 

Here is the combinatorial analysis for INS9 when dealt from an eight-deck shoe:

 

 

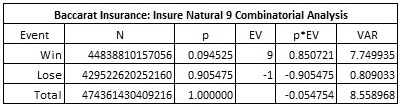
In particular,

• The house edge of INS9 is 5.4754%.
• The standard deviation of INS9 is 2.9256%.
• The hit frequency of INS9 is 9.4525%.

 

In analyzing INS9, there is one other very important statistic to keep in mind: the frequency with which the player has the opportunity to take the INS9 bet. For example, in blackjack, an Ace appears as the dealer’s up-card on average 1-in-13 cards (7.6923% of the hands). Therefore, in blackjack, the player has the opportunity to take blackjack insurance 7.6923% of the time. An AP will take blackjack insurance when an Ace is up and the count indicates he has the edge. Similarly, in baccarat, the frequency of a natural 9 is 9.4903%, and only a fraction of those hands will also correspond to a card counting edge for the AP.

 

In developing a card counting system for INS9, it appears obvious that the best system would be to count nines vs. other cards. The effect of removals shows that this is the case.

 

The following table gives the EOR’s for INS9:

 

 

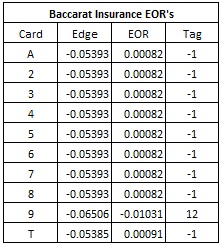
As shown in the table above, the best system to card count INS9 has tags (-1,-1,-1,-1,-1,-1,-1,-1,12,-1).

 

To determine the gain from card counting INS9, I simulated one billion (1,000,000,000) shoes of baccarat. I assumed the traditional cut card placement at 14 cards, and the usual burn-card rule at the start of each shoe. I assumed the AP made an INS9 wager whenever he had both the edge over the house, as determined by the count, and also the other hand was a natural 9.

 

Here are the results of this simulation:

 

 

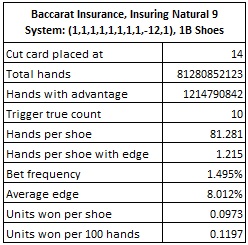
Note that the AP makes an INS9 wager on 1.495% of the hands. The condition that the first hand is also a natural 9 greatly reduces the frequency of INS9 wagers for the AP. If the AP was allowed to make the INS9 wager whenever the count indicated, instead of just those situations where the first hand is also a natural 9, then the AP would be making the INS9 wager on 15.751% of the hands.

 

The following table shows the card counting statistics for a variety of cut card placements from 14 cards to two decks. Each line was obtained by a simulation of one billion (1,000,000,000) shoes of baccarat.

 

 

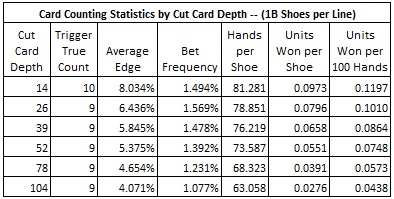
In my opinion, a win rate of 0.1197 units per 100 hands (with the cut card at 14 cards) makes INS9 a weak opportunity for the AP when compared to other baccarat side bets. But, keeping in mind that baccarat tables in Asia have extraordinarily high table limits, as well as the unclear limitations on the size of insurance bets that can be made, the profit potential from baccarat insurance may be significant.

 

Perhaps shoe-shopping can make the profit potential even higher. Recall that shoe-shopping means that the AP roams the casino watching for shoes where the first card dealt from the shoe is an Ace, meaning that only one unseen burn card is dealt. When the first card is an Ace, the best possible situation occurs in terms of the total number of cards seen in the shoe. However, it takes a great deal of time to shoe-shop, so the increased win must be significant before it becomes worthwhile.

 

The following table shows an AP who is both card-counting INS9 and is shoe-shopping for Aces:

 

 

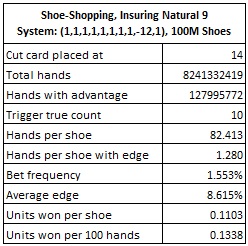
The shoe-shopper gets a return of 0.1338 units per 100 hands, compared to the play-all AP who has a return of 0.1197 units per 100 hands. Shoe-shopping generates 11.78% more profit. It is unlikely that this modest increase in profit makes up for the actual hands lost by shoe-shopping. In my opinion, shoe-shopping INS9 is not a viable method to increase the return for the AP.

 

What I don’t know at this point is if there are other bets in the insurance conglomerate that can also be card counted. If there are a number of insurance wagers that are similarly vulnerable, then perhaps a team can work together, each counting his particular insurance wager, signaling to the table when to take his particular insurance bet. This makes baccarat insurance potentially similar to the highly vulnerable UR Way Egalite baccarat side bet.

 

The recommendations for protecting INS9 from card counting are as follows:

• Watch for large insurance bets late in the shoe.
• Watch for players jumping into the shoe to make insurance bets.
• Watch for players who make insurance bets without making Player/Banker bets.
• Watch for team play.
• Consider the possible vulnerability of other insurance bets.

 

[Added September 12, 2013]

 

A reader asked if the count described in this post could also be used for the insurance bet on a natural 8 (INS8). When the first two cards are a natural 8, the player can insure that hand. INS8 pays 7-to-1 if the other hand is a natural 9, it pushes if the other hand is a natural 8, otherwise INS8 loses. The following combinatorial analysis shows a house edge of 14.635% for INS8.

 

 

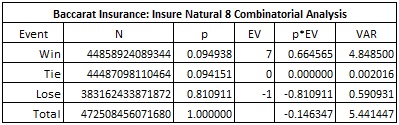
My immediate reaction when I saw these numbers is that there is no way that the count (-1,-1,-1,-1,-1,-1,-1,-1,12,-1) could generate an edge for the player over INS8. First, the large baseline edge of 14.635% is a lot to overcome for any count system, even in the best of circumstances. Second, the count system given above is probably not optimal. Nevertheless, I decided to check by running a simulation of one billion (1,000,000,000) shoes counting INS8, with the cut card placed at 14 cards.

 

The following table gives the results of this simulation:

 

 

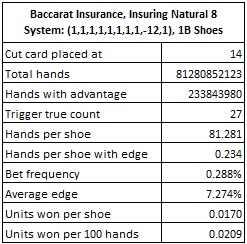
The AP can earn an extra 0.0209 units per 100 hands by using the count for INS9 for the INS8 bet. The AP makes the INS9 bet when the true count is +10 or higher, and he makes the INS8 bet when the true count is +27 or higher.

 

Recall that the AP can earn 0.1197 units per 100 hands against INS9. In total, then, the AP can earn 0.1197 + 0.0209 = 0.1406 units per 100 hands. This is a significant improvement over just counting INS9 alone.

 

[Added June 9, 2015]

 

The following tables were sent to me by a reader. These fill in the details about the various possible insurance bets some casinos offer. In particular, INS9 pays 8-to-1.