Card Counting the Dealer Bust 21 Blackjack Side Bet

By
|
|
Apheat, Side bets, Card Counting

At G2E (2013) this year I saw a side bet that seemed very familiar to me, Dealer Bust 21 (DB21), at the TCS John Huxley booth (as of August, 2016, DB21 is offered by AGS). DB21 is yet another blackjack side bet that pays if the dealer busts. This one has a unique distinction: I was the mathematician who did the original mathematical analysis. My report would normally be confidential, but in this case the inventor, Peter Blaine, decided to post my report on his game’s website (now defunct), so here it is. At the time I did this analysis (December, 2010), I was not routinely considering advantage play for games. I am therefore pleased that the results of this advantage play analysis did not expose negligence on my part. Nevertheless, DB21 is not risk-free.

 

The DB21 side bet is easy to understand. The player makes a DB21 wager before any cards are dealt. If the dealer has blackjack, all DB21 wagers lose. Otherwise, the players at the table finish playing their hands. The dealer then completes his hand to determine the dealer’s final result. If the dealer busts, the players who make DB21 wagers win according to a pay table, otherwise they lose. The payouts in the pay table are distinguished by the dealer’s up-card at the start of the hand. There is one oddity: if there are no players left with action (all players either busted or had blackjack), and a DB21 wager was made, then the dealer still has to play out his hand.

 

There are a number of pay tables for DB21. I am going to consider advantage play against the pay table with the lowest house edge. This pay table gives an upper bound on the vulnerability of DB21 to card counting.

 

The pay table considered here is:

 

  • Dealer up card = Ace, bust pays 15-to-1.
  • Dealer up card = 2, 3, 4, 5, 6, bust pays 1-to-1.
  • Dealer up card = 7, 8, 9, bust pays 2-to-1.
  • Dealer up card = Ten, Jack, Queen, King, bust pays 4-to-1.
  • Non-busted dealer hand loses.

 

This analysis assumes that the dealer hits soft 17 (H17) in every case.

 

The following table gives the combinatorial analysis for DB21 for two-decks:

 

the combinatorial analysis for DB21 for two-decks

 

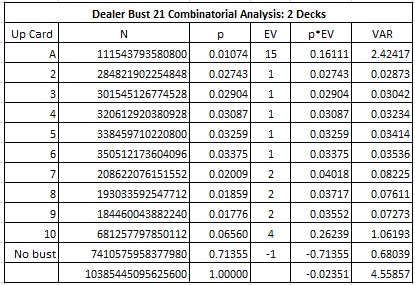
In particular:

 

  • The house edge is 2.351%.
  • The standard deviation is 2.135.
  • The hit frequency is 28.64%.

 

I don’t have much intuition about why DB21 should be vulnerable to card counting, or what cards are important. For example, it would be nice to have Aces in the deck because a dealer up-card of an Ace pays 15-to-1 if the dealer busts, so an Ace may be a good card for the counter. Conversely, hands with Aces are less likely to bust, so that an Ace may be a bad card for the counter if the dealer draws it mid-hand.

 

Before looking at the table below, ask yourself two questions:

 

  1. If an Ace is removed from the shoe, does the edge move towards the player or towards the house?
  2. Which card, if it is removed from the shoe, moves the edge towards the player by the greatest amount?

 

The following table gives the effect of removals (EORs) and a balanced card counting system based on these EORs for the two-deck game:

 

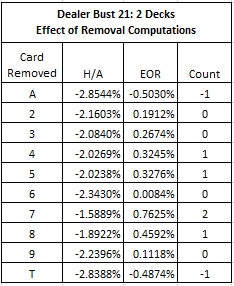
the effect of removals (EORs) and a balanced card counting system based on these EORs for the two-deck game - Dealer Bust 21: 2 Decks Effect os REmoval Computations

 

We see that Aces are the most valuable card for the house. Each time an Ace is dealt, the edge moves towards the house by about 0.50%. The card that moves the edge towards the player side by the greatest amount is a seven. Each time a seven is dealt, the edge moves towards the player side by about 0.76%. I do not have any intuition to explain this.

 

The card counting system developed here, (-1,0,0,1,1,0,2,1,0,-1) is not very accurate. It only weakly fits the EORs, with a betting correlation of only about 0.963 (the closer to 1, the better). A more complex system would perform better. If DB21 was highly vulnerable, it may be worth developing such a system, but that is not the case here.

 

The following table gives the results of simulating one billion (1,000,000,000) two-deck shoes, playing DB21 using the card counting system above:

 

the results of simulating one billion (1,000,000,000) two-deck shoes, playing DB21 - !B Shoes, Counting System: (-1,0,0,1,1,0,2,1,0,-1)

 

For the two-deck game, if an AP makes a $100 wager on DB21 whenever the true count is +3 or higher, and otherwise does not make a DB21 wager, then the AP will earn about $59.28 per 100 hands from the DB21 bet. The AP will make the DB21 wager on about 19.46% of the hands he plays, and when he makes the wager, his average edge over the house will be about 3.05%.

 

The following table gives the combinatorial analysis for DB21 for six-decks:

 

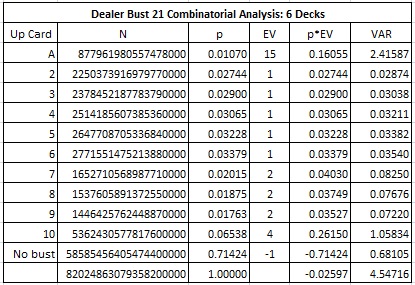
he combinatorial analysis for DB21 for six-decks - Dealer Bust Combinatorial Analysis: 6 Decks

 

In particular,

 

  • The house edge is 2.597%.
  • The standard deviation is 2.132.
  • The hit frequency is 28.58%.

 

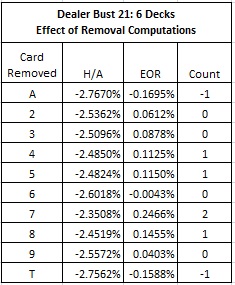
The following table gives the effect of EORs for the six-deck shoe game. Note how much smaller these EORs are than in the two-deck case. As usual, card counting is much less effective as the number of decks increases.  The card counting tags that are given here are the same as the two-deck game.

 

Dealer Bust 21: 6 Decks Effect of Removal Computations

 

The following table gives the results of simulating one billion (1,000,000,000) six-deck shoes, playing DB21 using the card counting system above:

 

the results of simulating one billion (1,000,000,000) six-deck shoes, playing DB21

 

For the six-deck game, if an AP makes a $100 wager on DB21 whenever the true count is +3 or higher, and otherwise does not make a DB21 wager, then the AP will earn about $23.22 per 100 hands from the DB21 bet. The AP will make the DB21 wager on about 12.28% of the hands he plays, and when he makes the wager, his average edge over the house will be about 1.89%.

 

There are several pay tables for DB21 that are much more challenging for the AP. The most common of these is the pay table that pays 10-to-1 for an Ace up-card (instead of 15-to-1), with every other payout the same as the pay table considered earlier. Here are the combinatorial statistics for this pay table:

 

  • House edge = 7.72%.
  • Standard deviation = 1.79.
  • Hit frequency = 28.64%.

 

The following are the results of a card counting simulation of one hundred million (100,000,000) two-deck shoes for this pay table:

 

  • Target true count = +11.
  • EV per bet = 1.824%.
  • Bet frequency = 1.798%.
  • Profit (in units) per 100 hands = 0.0328.

 

If an AP makes a $100 wager on DB21 whenever the true count is +11 or higher, and otherwise does not make a DB21 wager, then the AP will earn about $3.28 per 100 hands from the DB21 bet. The AP will make the DB21 wager on about 1.80% of the hands he plays, and when he makes the wager, his average edge over the house will be about 1.82%. This makes DB21 essentially worthless to the AP.

 

The variety of pay tables for DB21 yields a mixed bag of vulnerabilities to card counting. The most viable situation for the AP is in a two-deck game with the most liberal pay table considered earlier. In this case, DB21 is moderately vulnerable to card counting. But it quickly goes downhill from there. In just about any other situation, DB21 is minimally vulnerable to card counting.

 

Protecting DB21 from card counting is not urgent. But, a casino that offers the most liberal pay table on a two-deck game should definitely be aware of this possibility. A more reasoned approach is to be aware that every side bet is vulnerable, so casino staff should always pay attention.