Card Counting the Lucky Lucky Blackjack Side Bet

The “Lucky Lucky” (LL) blackjack side bet has payouts based on the player’s two cards and the dealer’s up-card. After the player makes the LL bet, the values of the player’s two cards and dealer’s up card are summed. Hands that total 19, 20 or 21 are winners, with bonuses for suited hands and for the hands 6-7-8 and 7-7-7. All other hands lose. As usual for blackjack, an Ace counts as 1 or 11. From 2009 through early 2012, this wager was licensed through Gaming Network, Inc. Unfortunately, Gaming Network dissolved in April of 2012. This wager is currently licensed through Aces Up Gaming.

 

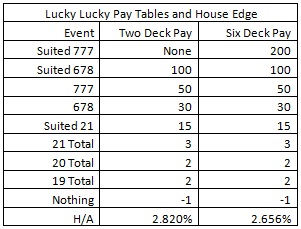
There are versions of the bet for both a double-deck game and a six-deck shoe. Here are the most common pay tables and the house edge for each:

 

 

The following table gives the effect of removal (EOR) for each card for the double-deck version of LL. This table shows the importance of the 6’s, 7’s and 8’s to player side. The Aces are also good for the player, mainly because of their dual role as a value of 1 or 11. This table also shows that the cards 2, 3 and T benefit the house so that the edge moves towards the player as they are played from the deck. The reason for this is intuitive.  First, the 2’s and 3’s are too small; it is hard to get a total up to 19 after being dealt these cards. Next, if the player is dealt a ten-valued card, then most likely his three-card total will exceed 21. The card counter likes it when there are a lot of A’s, 6’s, 7’s and 8’s in the deck. He doesn’t like it when there are a lot of 2’s, 3’s and T’s in the deck.

 

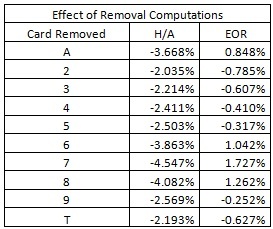
By looking at the column for EOR, I created a card counting system that assigns the 7’s a card counting value of -2 (negative two). To do this, I multiplied each value in the EOR column by 115.81 to get “System 1” with card counting tags (-0.98, 0.90, 0.70, 0.47, 0.37, -1.21, -2.00, -1.46, 0.29, 0.73). As usual for card counting systems, these tags are given in the order (A, 2, 3, 4, 5, 6, 7, 8, 9, T).

 

System 1 in not meant as a practical system. However, as a baseline counting system, it is worthwhile to see how it performs. In an effort to simplify this system, I also considered the balanced card counting system with tags (-1, 1, 1, 0, 0, -1, -2, -2, 0, 1). I’ll refer to this system as “System 2.” This system is easily used by a card counter of average skill level.

 

I wrote a computer program to simulate using these two systems in live play. My baseline simulation assumed a double-deck version of blackjack. For convenience, I’ll refer to the double-deck game as a “shoe.” After the cards in the shoe were shuffled, I assumed that the cut-card was placed after the 75-th card in the shoe. A burn card was dealt and the shoe was played out until the cut card came out. The shoe was then shuffled and the next shoe was simulated.

 

The following table gives the results of a simulation of one billion (1,000,000,000) shoes for each system.

 

 

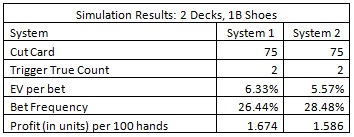
These simulations show that the card counter should make the LL wager whenever the true count is +2 or higher for the indicated system. With System 1, the player would have an average edge over the house of 6.33% whenever he made the bet and he would make the bet on 26.44% of the hands he played. The player would then win about 1.674 units per 100 blackjack hands. With System 2, the player has an average edge over the house of 5.57% whenever he makes the LL bet, and he would make the bet on 28.48% of the hands. The player would then win about 1.586 units per 100 blackjack hands.

 

As these results show, System 2 performs remarkably well compared to the nearly optimal System 1. To put this in perspective, if a person is playing head’s up double-deck, he may get as many as 200 rounds per hour. If the maximum allowed wager on LL is $100, then an advantage player will earn 1.586 x 2 x $100 = $317.27 per hour from card counting the LL wager.

 

The following table shows the player edge as a function of the true count for the double-deck version with the cut card placed at 75 cards, using System 2. The purpose of this analysis is to show how the player edge is correlated to the true count. These results are based on a simulation of one billion (1,000,000,000) shoes.

 

 

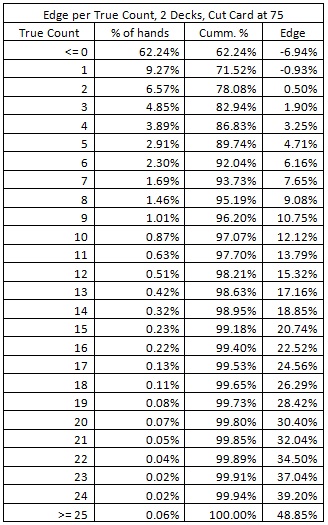
Compared to ordinary blackjack card counting, where the player edge reaches a theoretical maximum of about 5%, playing against LL can lead to some very large advantages.  The player gets an edge in excess of 10% on about 4% of his hands and an edge in excess of 20% on about 1% of his hands.  On about 5 hands per 10,000, the player will have an edge in excess of 40%.

 

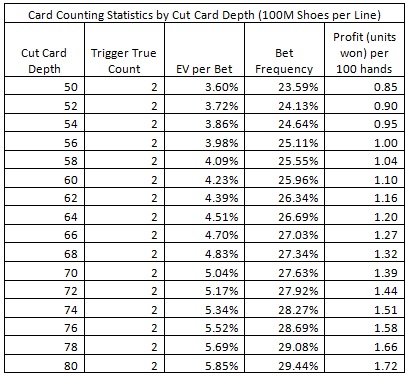
The natural defense a casino has towards a card counting form of advantage play is to position the cut card so that fewer cards are dealt between shuffles. The following table gives the EV per bet, bet frequency, and units won per 100 hands for cut card placements from 50 to 80 cards. Each row was arrived at by a simulation of one hundred million (100,000,000) shoes with the cut card placed at the indicated depth. As is evident from this table, the double-deck version of the LL wager is vulnerable to card counting, even at modest cut card placements. It follows that decreasing deck-penetration is not a viable way of protecting this wager.

 

 

It is worthwhile comparing these results to the six-deck version of the wager. For the six-deck game, a similar nearly perfect “System 1” was developed after computing the EOR for each card. It was then compared to the results from using System 2 (the same system as for two decks). System 2 once again performed exceptionally well. The following table gives the six-deck results for a cut card placed at 260 cards (1 deck cut off):

 

 

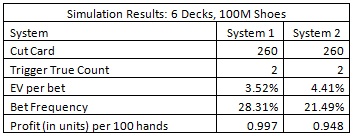
As can be seen from this table, the six-deck version is vulnerable and System 2 is a powerful system to use against it. However, even with a very deep cut card placement of 260 cards (52 cards cut off), the player’s edge is about the same as a mediocre placement of the cut card at 54 cards in the double-deck version. For this reason, a player who is targeting the LL side bet is much more likely to attack the double-deck version than the six-deck game. Because of this, I did not pursue the analysis of the six-deck version any further.

 

The Lucky Lucky side bet is extremely popular.  However, it has a significant vulnerability to card counting and that vulnerability needs to be addressed. Because an expert player will be giving up very little to the house on the main blackjack game, such a player can have great longevity flat betting and staying under the radar, while selectively betting LL on about 28% of his hands.  Such a player can easily produce a profit in excess of $200 per hour at a fast game with a limit of $100 on the LL bet.

 

The following are my recommendations for protecting the Lucky Lucky side bet:

 

• Change the game itself. If the developers change the pay tables to give a house edge in the 5% to 10% range, this would render card counting essentially ineffective.
• Maintain a low maximum wager for the Lucky Lucky side bet and require a bet of equal or greater size on blackjack.
• Lessening the deck penetration between shuffles has minimal effectiveness, and may be cost-negative due to a reduced number of rounds per hour for legitimate play. I recommend against this remedy.
• Watch for players who place large wagers on the Lucky Lucky side bet several rounds into the shoe but don’t make a wager on the first hand.
• Watch out for team play, that is, a table full of players who are betting the Lucky Lucky bet together.
• Watch for the other usual tells that a card counting system is being used.